Chapter 46
Introduction to Computational Biology
“In the field of observation, chance favors only the prepared mind.”\
- Louis Pasteur
Chapter 46 of CPVR introduces the fundamental concepts and computational techniques used in computational biology, with a focus on implementing these methods using Rust. The chapter covers a wide range of topics, from mathematical modeling and bioinformatics to systems biology, molecular dynamics, and drug discovery. Through practical examples and case studies, readers gain a deep understanding of how computational tools can be applied to analyze biological data, model complex biological systems, and contribute to advancements in fields such as genomics, neuroscience, and personalized medicine.
46.1. Foundations of Computational Biology
Computational biology is an interdisciplinary field that bridges biology, computer science, and mathematics to solve complex biological problems using computational methods. This convergence enables researchers to understand biological systems through mathematical models, simulations, and algorithmic analysis. Historically, biology relied heavily on experimental methods (wet-lab techniques) to uncover the intricacies of living organisms. However, with the explosion of biological data in recent decades, especially from high-throughput sequencing technologies, there is a need for more scalable, efficient, and precise computational techniques.
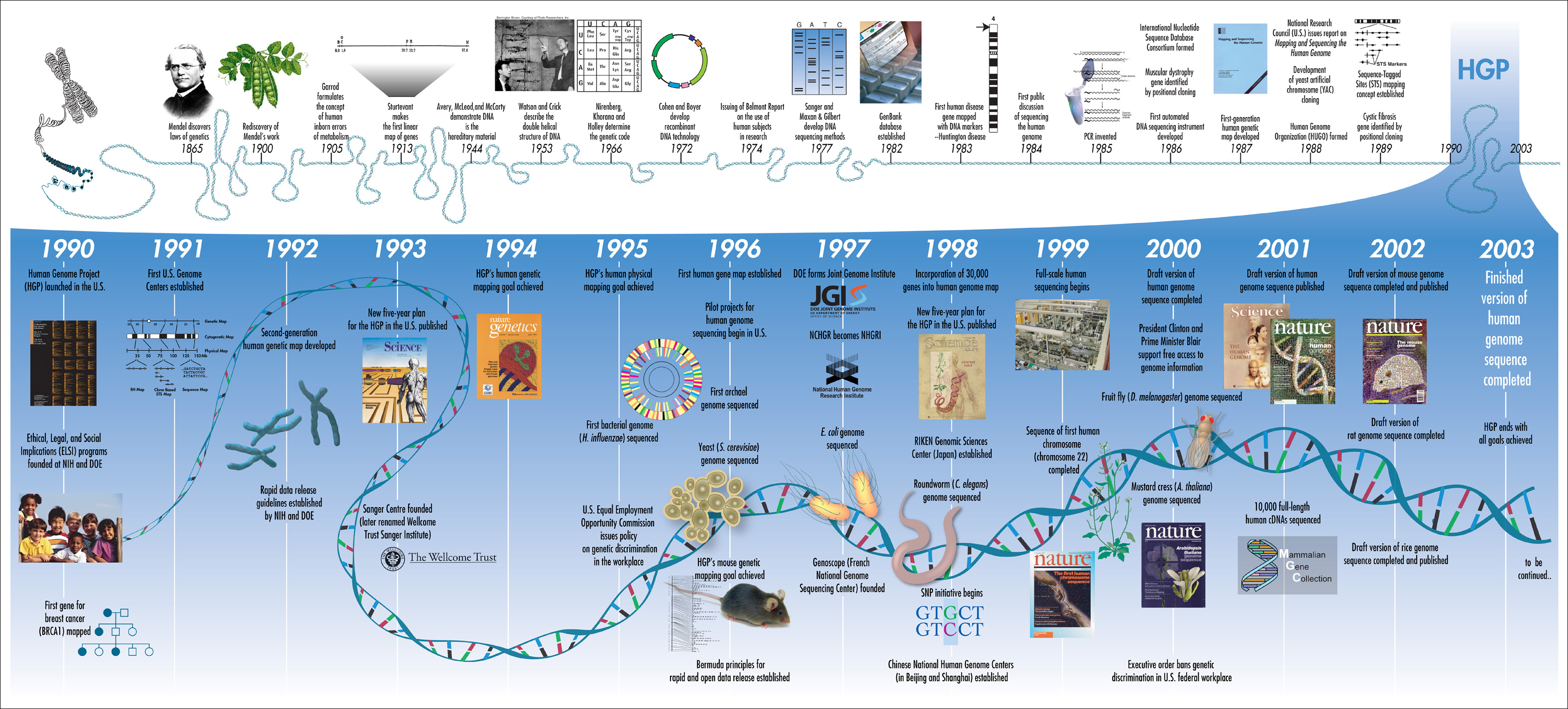
Historical journey of computational biology.
At the core of computational biology is the aim to model and simulate biological systems, ranging from molecular interactions to entire ecosystems. This involves building mathematical models that describe biological processes, then solving these models computationally to make predictions. As the field has evolved, various specialized areas have emerged, such as genomics, which focuses on analyzing the structure and function of genomes; proteomics, which looks at large-scale studies of proteins; and systems biology, which aims to understand how interactions between biological components give rise to complex behaviors in living organisms.
Key concepts in computational biology include sequence analysis, structural biology, systems biology, and molecular dynamics. Sequence analysis, for instance, is central to genomics, allowing researchers to align DNA, RNA, or protein sequences to find evolutionary relationships, identify genes, and predict functions. Structural biology focuses on understanding the three-dimensional structures of biological macromolecules like proteins and nucleic acids, which are crucial for understanding their function and interactions. Systems biology goes a step further by modeling how these molecules interact in networks that give rise to life’s complexity.
One of the critical shifts in biology has been the move from traditional experimental biology to in silico (computational) methods. While wet-lab experiments are still essential, computational models allow biologists to simulate complex phenomena that would be difficult or impossible to observe directly. For example, molecular dynamics simulations enable scientists to simulate the movement of atoms in a protein, providing insights into how it folds, functions, or interacts with other molecules. Computational methods also play a pivotal role in drug discovery, where they are used to screen millions of compounds to identify potential drugs efficiently.
Rust has emerged as a powerful language for computational biology due to its performance, safety, and concurrency features. Efficient handling of biological data often requires working with large datasets, high-performance computation, and parallel processing—all areas where Rust excels. Below is an example of how Rust can be used to implement a simple sequence alignment algorithm, a fundamental technique in computational biology:
/// Computes the global sequence alignment score between two sequences using the Needleman-Wunsch algorithm.
///
/// This function creates a scoring matrix that accounts for matches, mismatches, and gaps between
/// two sequences. It then fills the matrix using a dynamic programming approach to determine the
/// optimal alignment score.
///
/// # Arguments
///
/// * `seq1` - A string slice representing the first sequence.
/// * `seq2` - A string slice representing the second sequence.
///
/// # Returns
///
/// * An integer representing the alignment score between the two sequences.
fn needleman_wunsch(seq1: &str, seq2: &str) -> i32 {
// Convert sequences into vectors of characters for efficient access.
let seq1_chars: Vec<char> = seq1.chars().collect();
let seq2_chars: Vec<char> = seq2.chars().collect();
let m = seq1_chars.len();
let n = seq2_chars.len();
// Initialize a 2D vector to store alignment scores; dimensions are (m+1) x (n+1).
let mut score_matrix = vec![vec![0; n + 1]; m + 1];
// Set up the first column with gap penalties for the first sequence.
for i in 0..=m {
score_matrix[i][0] = i as i32 * -1;
}
// Set up the first row with gap penalties for the second sequence.
for j in 0..=n {
score_matrix[0][j] = j as i32 * -1;
}
// Populate the score matrix using dynamic programming.
for i in 1..=m {
for j in 1..=n {
// Determine the score based on whether the current characters match.
let match_score = if seq1_chars[i - 1] == seq2_chars[j - 1] { 1 } else { -1 };
// Calculate scores for diagonal (match/mismatch), upward (gap in seq2), and leftward (gap in seq1) moves.
let score_diag = score_matrix[i - 1][j - 1] + match_score;
let score_up = score_matrix[i - 1][j] - 1;
let score_left = score_matrix[i][j - 1] - 1;
// Select the maximum score among the calculated values.
score_matrix[i][j] = score_diag.max(score_up).max(score_left);
}
}
// Return the optimal alignment score located at the bottom-right of the matrix.
score_matrix[m][n]
}
fn main() {
// Define example sequences for alignment.
let seq1 = "AGCT";
let seq2 = "AGT";
// Calculate the alignment score using the Needleman-Wunsch algorithm.
let score = needleman_wunsch(seq1, seq2);
// Display the computed alignment score.
println!("Alignment score: {}", score);
}
This Rust code implements the Needleman-Wunsch algorithm for global sequence alignment. The algorithm aligns two sequences (seq1 and seq2) by constructing a scoring matrix that accounts for matches, mismatches, and gaps between the sequences. The matrix is initialized, and then filled by considering the match score (1 for a match, -1 for a mismatch) and penalties for inserting gaps (set to -1). The dynamic programming approach used here ensures an efficient calculation of the optimal alignment.
The code begins by creating a 2D vector score_matrix to store the scores of possible alignments. Initialization ensures that gaps at the start of the sequences are handled by penalizing the alignment. The core of the algorithm iterates over each character in the sequences, updating the score matrix based on matches, mismatches, and gaps. The final alignment score is returned as the value at the bottom-right of the matrix, representing the optimal alignment.
In a practical computational biology setting, this basic sequence alignment algorithm can be extended with optimizations for parallel processing or larger datasets. Rust’s safety guarantees, such as preventing data races in concurrent applications, make it well-suited for building such scalable tools in bioinformatics.
Moreover, Rust's ownership model and zero-cost abstractions help manage memory efficiently, which is critical in handling large genomic datasets. For instance, a genome assembly tool might need to process terabytes of sequence data, where memory management becomes crucial to prevent performance bottlenecks or crashes. Rust’s control over low-level memory operations allows fine-tuned performance, making it a great fit for computational biology tasks that require high efficiency and scalability.
By using Rust, computational biologists can not only build high-performance algorithms for tasks like sequence alignment, molecular simulations, or network analysis but also ensure that these programs run safely and efficiently, even at large scales. This makes Rust a promising tool for the next generation of computational biology software.
46.2. Mathematical Models in Biology
Mathematical models are a cornerstone of computational biology, offering a formal framework to describe, predict, and understand complex biological phenomena. These models can be broadly categorized into deterministic and stochastic types. Deterministic models, such as those based on differential equations, operate under the assumption that a system's behavior is completely determined by its initial conditions and parameters. For instance, the interaction between predator and prey populations can be described by ordinary differential equations where the future state of the system is entirely defined by its current state and the rate of change.
In contrast, stochastic models embrace the inherent randomness and variability present in biological systems. Many processes, such as gene expression or molecular interactions, display probabilistic behavior due to the discrete and random nature of biochemical events. In such cases, models like Markov processes or the Gillespie algorithm are more appropriate to capture the uncertainty and fluctuations observed in biological phenomena. For example, the Gillespie algorithm is used to simulate the time evolution of chemical reactions in small molecular populations, which is particularly relevant for cellular processes where the number of molecules is low and subject to random variations.
Mathematical models are indispensable tools for describing a wide range of biological phenomena, including population dynamics, enzyme kinetics, and gene regulatory networks. In the study of population dynamics, deterministic models such as the Lotka-Volterra equations provide insight into how species interact over time, often revealing oscillatory behavior or equilibrium states that are crucial for understanding ecosystem stability. Enzyme kinetics can be modeled using equations like Michaelis-Menten, which describe how reaction rates are influenced by substrate concentrations. These models help elucidate the catalytic mechanisms of enzymes and the impact of substrate saturation on reaction velocities.
Stochastic models play a vital role in capturing the uncertainty intrinsic to biological systems. Gene regulatory networks, for example, frequently display stochastic behavior due to the random binding events of transcription factors to DNA. This randomness can lead to significant cell-to-cell variability in gene expression even among genetically identical cells. Stochastic models provide a means to quantify these fluctuations and are essential for understanding processes such as gene regulation and cellular differentiation, where variability has profound biological implications.
Rust is an excellent choice for implementing both deterministic and stochastic models in biology because of its performance, safety, and concurrency features. The following examples illustrate how Rust can be used to implement a simple deterministic model using the Lotka-Volterra predator-prey equations and a stochastic model using the Gillespie algorithm.
/// Computes the next state of prey and predator populations using the Lotka-Volterra equations.
///
/// This function calculates the growth of the prey population based on its natural growth rate
/// and its reduction due to predation. Similarly, it calculates the growth of the predator population
/// based on the available prey and its natural death rate. The function uses a simple Euler method
/// for time integration.
///
/// # Arguments
///
/// * `prey` - Current population of the prey species.
/// * `predator` - Current population of the predator species.
/// * `a` - Natural growth rate of the prey.
/// * `b` - Predation rate coefficient.
/// * `c` - Reproduction rate of predators per prey consumed.
/// * `d` - Natural death rate of predators.
/// * `dt` - Time step for the simulation.
///
/// # Returns
///
/// * A tuple containing the updated populations of prey and predator.
fn lotka_volterra(prey: f64, predator: f64, a: f64, b: f64, c: f64, d: f64, dt: f64) -> (f64, f64) {
// Calculate the rate of change for the prey population.
let prey_growth = a * prey - b * prey * predator;
// Calculate the rate of change for the predator population.
let predator_growth = c * prey * predator - d * predator;
// Update populations using Euler integration.
(prey + prey_growth * dt, predator + predator_growth * dt)
}
fn main() {
// Initialize the populations and parameters for the Lotka-Volterra model.
let (mut prey, mut predator) = (40.0, 9.0);
let (a, b, c, d, dt) = (0.1, 0.02, 0.01, 0.1, 0.1);
// Run the simulation for 1000 time steps.
for _ in 0..1000 {
let (new_prey, new_predator) = lotka_volterra(prey, predator, a, b, c, d, dt);
prey = new_prey;
predator = new_predator;
println!("Prey: {:.2}, Predator: {:.2}", prey, predator);
}
}
In this deterministic model, the Lotka-Volterra equations capture the interaction between prey and predator populations. The prey population grows naturally but is reduced by predation, while the predator population increases based on prey availability and decreases due to natural mortality. The simulation, executed over 1,000 time steps, updates the populations using Euler integration. Rust's robust handling of numerical calculations makes it well-suited for such simulations, allowing for extensions to more complex models or longer time scales.
/// Simulates a simple biochemical reaction using the Gillespie algorithm.
///
/// This function computes the time until the next reaction occurs based on the total reaction rate,
/// and then randomly selects which reaction takes place using an exponential distribution. The molecule
/// counts are updated accordingly. Two reversible reactions are modeled: A converting to B and B converting
/// back to A.
///
/// # Arguments
///
/// * `reaction_rates` - Slice containing the reaction rates for each reaction.
/// * `molecule_counts` - Mutable slice containing the counts of molecules involved in the reactions.
/// * `dt` - Maximum allowable time step for the simulation.
///
/// # Returns
///
/// * A floating-point value representing the time step until the next reaction occurs.
extern crate rand;
use rand::Rng;
fn gillespie(reaction_rates: &[f64], molecule_counts: &mut [i32], dt: f64) -> f64 {
// Initialize a random number generator.
let mut rng = rand::thread_rng();
// Calculate the total reaction rate by summing individual reaction rates.
let total_rate: f64 = reaction_rates.iter().sum();
// Generate a random time interval tau using an exponential distribution.
let tau = -1.0 / total_rate * (rng.gen::<f64>().ln());
// Determine which reaction occurs by selecting an event based on the cumulative rate.
let mut cumulative_rate = 0.0;
let rand_event = rng.gen::<f64>() * total_rate;
for (i, &rate) in reaction_rates.iter().enumerate() {
cumulative_rate += rate;
if cumulative_rate > rand_event {
// Update molecule counts based on the selected reaction.
match i {
0 => molecule_counts[0] -= 1, // Reaction: A -> B
1 => molecule_counts[0] += 1, // Reaction: B -> A
_ => (),
}
break;
}
}
// Return the smaller of the computed tau and the provided dt.
tau.min(dt)
}
fn main() {
// Set initial molecule counts for species A and B.
let mut molecule_counts = [100, 50];
// Define the reaction rates for the two reversible reactions: A -> B and B -> A.
let reaction_rates = [1.0, 0.5];
let dt = 0.1;
// Run the simulation for 100 iterations.
for _ in 0..100 {
let tau = gillespie(&reaction_rates, &mut molecule_counts, dt);
println!("A: {}, B: {}, Tau: {:.2}", molecule_counts[0], molecule_counts[1], tau);
}
}
This stochastic model uses the Gillespie algorithm to simulate biochemical reactions where random events determine the system's evolution. The code computes the time interval until the next reaction, selects the reaction based on the cumulative probability of each reaction occurring, and updates the molecule counts accordingly. Rust’s built-in random number generation and efficient control over memory make it an ideal choice for such simulations, ensuring that the program can handle the inherent randomness of molecular interactions.
Rust’s performance, combined with its safety features such as ownership and borrowing, makes it particularly suited for numerical computations in computational biology. Whether handling deterministic models like the Lotka-Volterra equations or stochastic models like the Gillespie algorithm, Rust provides the necessary tools to build robust, efficient, and scalable simulations. This capability is essential for advancing our understanding of complex biological systems, from ecosystem dynamics and enzyme kinetics to gene regulatory networks and cellular processes.
46.3. Bioinformatics and Sequence Analysis
Bioinformatics is a rapidly growing field that plays a critical role in biological research, particularly in the analysis of DNA, RNA, and protein sequences. The vast amount of biological sequence data generated by modern technologies such as next-generation sequencing (NGS) has made computational tools essential for handling, analyzing, and interpreting this data. Sequence analysis lies at the heart of bioinformatics, allowing researchers to explore and understand the genetic information encoded in organisms. This includes tasks such as gene identification, functional annotation, protein structure prediction, and evolutionary studies.
Sequence analysis techniques include sequence alignment, motif discovery, and phylogenetic analysis. Sequence alignment is a foundational method that involves arranging sequences to identify regions of similarity, which may indicate functional, structural, or evolutionary relationships between the sequences. Algorithms such as Needleman-Wunsch and Smith-Waterman are commonly used for global and local alignments, respectively. Motif discovery aims to identify short, recurring patterns in sequences that may be biologically significant, such as binding sites for proteins. Phylogenetic analysis, on the other hand, focuses on reconstructing evolutionary relationships between organisms or genes, providing insights into how species or genes have diverged over time.
The importance of sequence analysis in bioinformatics cannot be overstated. DNA, RNA, and protein sequences contain the fundamental information that governs the functioning of all living organisms. By analyzing these sequences, researchers can identify genes, predict the structure and function of proteins, and understand evolutionary relationships between species. For example, sequence alignment allows scientists to compare a newly discovered gene with known sequences to infer its function based on similarity. Protein structure prediction relies on sequence information to model how a protein will fold, which in turn helps understand its function.
Phylogenetic tree construction is another key aspect of bioinformatics, allowing researchers to explore the evolutionary history of genes or species. By comparing sequences across different organisms, scientists can build trees that illustrate the evolutionary divergence and relationships between species. This is crucial in evolutionary biology, as it helps to trace the ancestry of genes and organisms, revealing insights into how life has evolved over millions of years.
Rust offers powerful features for implementing bioinformatics algorithms due to its performance, memory safety, and concurrency. Below, we will discuss the implementation of two critical algorithms: Needleman-Wunsch for global sequence alignment and the Hidden Markov Model (HMM) for sequence classification.
The Needleman-Wunsch algorithm is used for global alignment, aligning two sequences from start to finish. It constructs a scoring matrix where the optimal alignment is computed by maximizing the alignment score while considering penalties for mismatches and gaps. Here’s how it can be implemented in Rust:
/// Computes the optimal global sequence alignment between two sequences using the Needleman-Wunsch algorithm.
///
/// This function creates and fills a scoring matrix that accounts for match rewards, mismatch penalties,
/// and gap penalties. It then performs a traceback to construct the aligned sequences.
///
/// # Arguments
///
/// * `seq1` - A string slice representing the first sequence.
/// * `seq2` - A string slice representing the second sequence.
/// * `match_score` - The score to assign for a character match.
/// * `mismatch_penalty` - The penalty for a character mismatch.
/// * `gap_penalty` - The penalty for introducing a gap in the alignment.
///
/// # Returns
///
/// * A tuple containing the final alignment score, the aligned first sequence, and the aligned second sequence.
fn needleman_wunsch(seq1: &str, seq2: &str, match_score: i32, mismatch_penalty: i32, gap_penalty: i32) -> (i32, String, String) {
// Determine the lengths of the sequences.
let m = seq1.len();
let n = seq2.len();
// Create a scoring matrix initialized with zeros.
let mut score_matrix = vec![vec![0; n + 1]; m + 1];
// Create a traceback matrix to record the path taken for alignment.
let mut traceback = vec![vec![(0, 0); n + 1]; m + 1];
// Initialize the first column of the scoring matrix with gap penalties.
for i in 0..=m {
score_matrix[i][0] = i as i32 * gap_penalty;
}
// Initialize the first row of the scoring matrix with gap penalties.
for j in 0..=n {
score_matrix[0][j] = j as i32 * gap_penalty;
}
// Fill the scoring matrix using dynamic programming.
for i in 1..=m {
for j in 1..=n {
// Determine if the current characters match or mismatch.
let current_char_seq1 = seq1.chars().nth(i - 1).unwrap();
let current_char_seq2 = seq2.chars().nth(j - 1).unwrap();
let score_diag = score_matrix[i - 1][j - 1] +
if current_char_seq1 == current_char_seq2 { match_score } else { mismatch_penalty };
// Calculate the score for introducing a gap in seq2.
let score_up = score_matrix[i - 1][j] + gap_penalty;
// Calculate the score for introducing a gap in seq1.
let score_left = score_matrix[i][j - 1] + gap_penalty;
// Choose the maximum score among the three possible moves.
score_matrix[i][j] = score_diag.max(score_up).max(score_left);
// Record the traceback direction based on the maximum score.
if score_matrix[i][j] == score_diag {
traceback[i][j] = (i - 1, j - 1);
} else if score_matrix[i][j] == score_up {
traceback[i][j] = (i - 1, j);
} else {
traceback[i][j] = (i, j - 1);
}
}
}
// Trace back from the bottom-right corner of the matrix to reconstruct the aligned sequences.
let mut aligned_seq1 = String::new();
let mut aligned_seq2 = String::new();
let (mut i, mut j) = (m, n);
while i > 0 || j > 0 {
let (prev_i, prev_j) = traceback[i][j];
if prev_i == i - 1 && prev_j == j - 1 {
aligned_seq1.push(seq1.chars().nth(i - 1).unwrap());
aligned_seq2.push(seq2.chars().nth(j - 1).unwrap());
} else if prev_i == i - 1 {
aligned_seq1.push(seq1.chars().nth(i - 1).unwrap());
aligned_seq2.push('-');
} else {
aligned_seq1.push('-');
aligned_seq2.push(seq2.chars().nth(j - 1).unwrap());
}
i = prev_i;
j = prev_j;
}
// Reverse the strings since the traceback builds the alignment from the end to the beginning.
(
score_matrix[m][n],
aligned_seq1.chars().rev().collect(),
aligned_seq2.chars().rev().collect()
)
}
fn main() {
// Define the sequences to be aligned.
let seq1 = "GATTACA";
let seq2 = "GCATGCU";
// Call the Needleman-Wunsch function with specified match, mismatch, and gap penalties.
let (score, aligned_seq1, aligned_seq2) = needleman_wunsch(seq1, seq2, 1, -1, -2);
// Output the alignment score and the aligned sequences.
println!("Alignment score: {}", score);
println!("Aligned Seq1: {}", aligned_seq1);
println!("Aligned Seq2: {}", aligned_seq2);
}
In this Rust implementation of the Needleman-Wunsch algorithm, we first initialize a scoring matrix and then fill it based on match/mismatch and gap penalties. After calculating the optimal alignment, we backtrack through the matrix to generate the aligned sequences. Rust’s memory safety and performance allow this alignment to be computed efficiently, even for large sequences.
Hidden Markov Models (HMMs) are widely used for sequence classification tasks, such as recognizing patterns in DNA sequences or annotating regions in genomes. Below is a simplified example of implementing an HMM in Rust:
/// Defines a simple Hidden Markov Model (HMM) for sequence classification and implements the Viterbi algorithm.
///
/// The HMM consists of a set of states, initial state probabilities, transition probabilities between states,
/// and emission probabilities that relate states to observable symbols. The Viterbi algorithm computes the
/// most probable sequence of hidden states given an observed sequence.
///
/// # Fields
///
/// * `states` - A vector of characters representing the hidden states.
/// * `start_prob` - A vector of initial probabilities for each state.
/// * `trans_prob` - A 2D vector representing the probabilities of transitioning between states.
/// * `emission_prob` - A 2D vector representing the probabilities of emitting each observable symbol from a state.
struct HMM {
states: Vec<char>,
start_prob: Vec<f64>,
trans_prob: Vec<Vec<f64>>,
emission_prob: Vec<Vec<f64>>,
}
impl HMM {
/// Applies the Viterbi algorithm to determine the most likely sequence of states for the observed sequence.
///
/// # Arguments
///
/// * `observed` - A slice of characters representing the observed sequence (e.g., DNA bases).
///
/// # Returns
///
/// * A vector of characters representing the most probable sequence of hidden states.
fn viterbi(&self, observed: &[char]) -> Vec<char> {
let num_states = self.states.len();
let seq_length = observed.len();
// Initialize dynamic programming matrix to store probabilities.
let mut dp = vec![vec![0.0; seq_length]; num_states];
// Initialize a matrix to store the best previous state for each state at each time step.
let mut path = vec![vec![0; seq_length]; num_states];
// Initialization: calculate the probability for the first observation for each state.
for i in 0..num_states {
dp[i][0] = self.start_prob[i] * self.emission_prob[i][self.index_of(observed[0])];
path[i][0] = i;
}
// Iterate over the observed sequence starting from the second element.
for t in 1..seq_length {
for i in 0..num_states {
let mut max_prob = 0.0;
let mut best_state = 0;
// Evaluate each possible previous state.
for j in 0..num_states {
let prob = dp[j][t - 1] * self.trans_prob[j][i] *
self.emission_prob[i][self.index_of(observed[t])];
if prob > max_prob {
max_prob = prob;
best_state = j;
}
}
dp[i][t] = max_prob;
path[i][t] = best_state;
}
}
// Identify the state with the highest probability at the final time step.
let mut best_final_state = 0;
let mut max_prob = 0.0;
for i in 0..num_states {
if dp[i][seq_length - 1] > max_prob {
max_prob = dp[i][seq_length - 1];
best_final_state = i;
}
}
// Trace back through the path matrix to reconstruct the most probable state sequence.
let mut result = vec![' '; seq_length];
let mut prev_state = best_final_state;
for t in (0..seq_length).rev() {
result[t] = self.states[prev_state];
prev_state = path[prev_state][t];
}
result
}
/// Converts an observable symbol to its corresponding index used in the emission probability matrix.
///
/// # Arguments
///
/// * `symbol` - A character representing an observable symbol (e.g., 'A', 'C', 'G', 'T').
///
/// # Returns
///
/// * An unsigned integer index corresponding to the symbol.
fn index_of(&self, symbol: char) -> usize {
match symbol {
'A' => 0,
'C' => 1,
'G' => 2,
'T' => 3,
_ => panic!("Invalid symbol encountered in observed sequence"),
}
}
}
fn main() {
// Define a simple HMM with two hidden states.
let hmm = HMM {
states: vec!['E', 'I'], // For example, 'E' might represent an exon and 'I' an intron.
start_prob: vec![0.5, 0.5],
trans_prob: vec![
vec![0.5, 0.5],
vec![0.4, 0.6],
],
emission_prob: vec![
vec![0.25, 0.25, 0.25, 0.25], // Equal probability for A, C, G, T in state 'E'
vec![0.4, 0.1, 0.4, 0.1], // Different emission probabilities in state 'I'
],
};
// Define an observed sequence of DNA bases.
let observed = vec!['G', 'A', 'T', 'T', 'A', 'C', 'A'];
// Apply the Viterbi algorithm to determine the most likely sequence of hidden states.
let result = hmm.viterbi(&observed);
// Output the result.
println!("Most likely states: {:?}", result);
}
This code implements the Viterbi algorithm for sequence classification using an HMM. The algorithm calculates the most probable sequence of hidden states given an observed sequence (in this case, DNA bases). The HMM is defined with states, start probabilities, transition probabilities, and emission probabilities. The Viterbi algorithm then uses dynamic programming to compute the most probable state path through the sequence.
When handling large sequence datasets, Rust’s performance advantages become even more apparent. Rust’s zero-cost abstractions and efficient memory management ensure that bioinformatics algorithms, such as sequence alignment or HMMs, can scale to handle massive datasets without running into performance bottlenecks commonly found in higher-level languages. Rust’s concurrency model also allows for parallel processing of sequence data, further speeding up large-scale bioinformatics computations.
By leveraging Rust’s powerful features, bioinformatics applications can be built that are not only efficient but also safe and reliable, making Rust an excellent choice for developing the next generation of bioinformatics tools.
46.4. Systems Biology and Network Modeling
Systems biology is an interdisciplinary field dedicated to understanding biological systems by examining the intricate interactions among their components instead of focusing solely on individual parts. This holistic approach enables researchers to study how molecules, cells, and tissues interact and cooperate to produce complex behaviors such as metabolism, gene regulation, and signal transduction. By representing these interactions as networks, systems biology offers a framework to investigate emergent properties—phenomena that cannot be explained by the behavior of individual components alone but arise from their collective interplay.
Network modeling is a powerful technique in systems biology, facilitating the representation of complex biological systems as interconnected networks. Such networks may represent metabolic pathways that describe biochemical reactions, protein-protein interaction networks that capture the physical contacts between proteins, or gene regulatory networks that delineate the regulatory relationships among genes and their products. Analysis of these networks provides deep insights into how biological systems are organized and function, revealing mechanisms of robustness, adaptability, and homeostasis that allow systems to withstand perturbations and adjust to new environmental conditions.
The study of biological networks yields critical insights into emergent properties. Robustness, for example, reflects a system’s capacity to maintain functionality in the face of disturbances such as mutations or external stress. In a gene regulatory network, redundant pathways or feedback loops may ensure that the system continues to operate even when some components are compromised. Similarly, adaptability allows biological systems to modify their behavior in response to changing conditions, as seen in metabolic networks that reroute biochemical pathways when nutrient levels fluctuate.
Network modeling is also integral to synthetic biology, where researchers design and engineer biological systems to exhibit desired functionalities. Synthetic gene regulatory networks, for example, can be constructed to produce specific outputs such as the synthesis of therapeutic compounds. In these applications, the ability to simulate and predict system behavior using computational models is essential for verifying design principles before experimental implementation.
Rust is particularly well-suited for network modeling in systems biology due to its exceptional performance, robust memory safety, and support for concurrency. The example below illustrates how to model a simple gene regulatory network in Rust. In this model, the interaction between two genes is simulated, where the expression level of one gene (Gene A) inhibits the expression of another gene (Gene B), establishing a negative feedback loop that is commonly observed in biological regulation.
/// Simulates the dynamics of a simple gene regulatory network where Gene A inhibits Gene B.
///
/// In this model, Gene A produces a factor that represses the expression of Gene B. The production
/// rates are represented by nonlinear functions that capture the inhibitory effect, while degradation
/// rates are assumed to be proportional to the current expression levels. The simulation uses Euler
/// integration to update gene expression levels over a given time step.
///
/// # Arguments
///
/// * `gene_a` - The current expression level of Gene A.
/// * `gene_b` - The current expression level of Gene B.
/// * `k1` - The production rate constant for Gene A, modulated by inhibition from Gene B.
/// * `k2` - The production rate constant for Gene B, modulated by inhibition from Gene A.
/// * `dt` - The time step for numerical integration.
///
/// # Returns
///
/// * A tuple containing the updated expression levels of Gene A and Gene B.
fn gene_regulation(gene_a: f64, gene_b: f64, k1: f64, k2: f64, dt: f64) -> (f64, f64) {
// Calculate the production rate for Gene A with inhibition by Gene B.
let production_a = k1 / (1.0 + gene_b);
// Degradation of Gene A is proportional to its current level.
let degradation_a = gene_a;
// Calculate the production rate for Gene B with inhibition by Gene A.
let production_b = k2 / (1.0 + gene_a);
// Degradation of Gene B is proportional to its current level.
let degradation_b = gene_b;
// Update the expression levels using Euler integration.
let new_gene_a = gene_a + (production_a - degradation_a) * dt;
let new_gene_b = gene_b + (production_b - degradation_b) * dt;
(new_gene_a, new_gene_b)
}
fn main() {
// Initialize the expression levels for Gene A and Gene B.
let mut gene_a = 1.0;
let mut gene_b = 0.5;
// Set the production rate constants and the integration time step.
let (k1, k2, dt) = (2.0, 1.5, 0.01);
// Run the simulation for 1000 time steps.
for _ in 0..1000 {
let (new_gene_a, new_gene_b) = gene_regulation(gene_a, gene_b, k1, k2, dt);
gene_a = new_gene_a;
gene_b = new_gene_b;
println!("Gene A: {:.2}, Gene B: {:.2}", gene_a, gene_b);
}
}
In this gene regulatory model, the concentration of Gene A acts to repress Gene B and vice versa, representing a negative feedback loop. The production terms are modulated by the presence of the inhibitory gene product, while degradation is modeled as a simple linear process. The simulation updates the expression levels using a straightforward Euler integration method over 1000 time steps.
Another essential aspect of network modeling in systems biology is the simulation of metabolic networks. The following example demonstrates how to model a small metabolic pathway where a substrate A is converted to an intermediate B, which is then converted to a product C. This sequential reaction model captures the dynamics of substrate consumption and product formation.
/// Simulates a simple metabolic pathway involving two consecutive reactions: A -> B -> C.
///
/// In this model, the conversion of substrate A to intermediate B is governed by a rate constant k1,
/// while the conversion of B to product C is governed by a rate constant k2. The changes in concentrations
/// are calculated using Euler integration over a specified time step.
///
/// # Arguments
///
/// * `a` - The current concentration of substrate A.
/// * `b` - The current concentration of intermediate B.
/// * `c` - The current concentration of product C.
/// * `k1` - The rate constant for the reaction A -> B.
/// * `k2` - The rate constant for the reaction B -> C.
/// * `dt` - The time step for the simulation.
///
/// # Returns
///
/// * A tuple containing the updated concentrations of A, B, and C.
fn metabolic_pathway(a: f64, b: f64, c: f64, k1: f64, k2: f64, dt: f64) -> (f64, f64, f64) {
// Calculate the reaction rate for A -> B.
let reaction1 = k1 * a;
// Calculate the reaction rate for B -> C.
let reaction2 = k2 * b;
// Update the concentration of A, decreasing due to its conversion to B.
let new_a = a - reaction1 * dt;
// Update the concentration of B, which is produced from A and consumed to form C.
let new_b = b + (reaction1 - reaction2) * dt;
// Update the concentration of C, which is formed from the conversion of B.
let new_c = c + reaction2 * dt;
(new_a, new_b, new_c)
}
fn main() {
// Initialize the concentrations for metabolites A, B, and C.
let mut a = 1.0;
let mut b = 0.0;
let mut c = 0.0;
// Set the reaction rate constants and the simulation time step.
let (k1, k2, dt) = (1.0, 0.5, 0.01);
// Run the simulation for 1000 time steps.
for _ in 0..1000 {
let (new_a, new_b, new_c) = metabolic_pathway(a, b, c, k1, k2, dt);
a = new_a;
b = new_b;
c = new_c;
println!("A: {:.2}, B: {:.2}, C: {:.2}", a, b, c);
}
}
This metabolic pathway model simulates the transformation of substrate A into intermediate B and subsequently into product C. The reaction rates depend on the current concentrations of the reactants, and Euler integration is used to update these concentrations over discrete time steps. Such models are fundamental in understanding how metabolic fluxes change over time and can be scaled to encompass more complex networks involving numerous reactions and metabolites.
Rust’s combination of performance, safety, and concurrency makes it an ideal choice for constructing scalable network models in systems biology. The language's low-level memory control and safe concurrency allow for efficient parallel computation, making it possible to simulate large-scale biological networks, such as genome-wide regulatory networks or comprehensive metabolic pathways, without sacrificing reliability. These attributes are particularly beneficial when dealing with simulations that require handling thousands of reactions or complex interdependencies among network nodes.
Overall, by leveraging Rust for network modeling, researchers can develop robust and efficient simulations that accurately represent the emergent properties of biological systems. Whether simulating gene regulatory networks, protein interactions, or metabolic pathways, Rust provides the necessary tools to explore the dynamics of these complex systems and to advance our understanding of their underlying principles in systems biology and synthetic biology applications.
46.5. Molecular Dynamics and Structural Biology
Molecular Dynamics (MD) simulations serve as a crucial instrument in structural biology, allowing researchers to investigate the movement of atoms and molecules over time with remarkable detail. These simulations are essential for understanding the physical behavior of biological macromolecules such as proteins, nucleic acids, and lipid membranes. By applying classical mechanics, MD simulations model the interactions between atoms and track their trajectories as forces act upon them. The fundamental principle involves numerically solving Newton’s equations of motion for each atom in the system, thereby providing an in-depth, time-resolved view of molecular behavior.
Within structural biology, MD simulations are invaluable for exploring phenomena like protein folding, where a protein transitions from an unfolded chain of amino acids into its functional three-dimensional structure. Such simulations elucidate the dynamics of molecular interactions, for instance, how a ligand binds to a receptor—a process that is critical in drug discovery. By capturing the complex movements of molecules, MD simulations enable the prediction of interaction patterns and shed light on the relationship between molecular structure and function.
Another significant application of MD simulations is the study of lipid bilayers and membrane dynamics. Biological membranes, which are primarily composed of lipid bilayers, play an essential role in cell function and signaling. MD simulations provide insight into the behavior of these membranes by examining how proteins and small molecules interact with them, how membranes self-assemble, and how they respond to variations in their environment. This dynamic perspective is crucial, as macromolecules such as proteins and nucleic acids continuously undergo conformational changes that are fundamental to their biological roles.
The detailed investigation of molecular motions is particularly important for proteins, nucleic acids, and lipid membranes because these structures are inherently dynamic. For example, proteins do not remain static but instead experience conformational shifts that are essential for enzymatic activity, signal transduction, and substrate binding. Similarly, the flexibility and dynamic behavior of DNA and RNA impact processes like transcription and replication, while the fluidity of lipid membranes is key to forming vesicles and lipid rafts. MD simulations thus offer high-resolution, time-dependent insights into the intricate movements and interactions that govern biological systems.
Rust’s high-performance capabilities make it an excellent choice for implementing MD simulations. The following example illustrates a simplified MD simulation for a system of particles interacting via the Lennard-Jones potential. This foundational model can serve as a stepping stone toward more complex simulations, such as those modeling protein folding or lipid bilayer dynamics.
use std::f64::consts::PI;
/// Structure representing a particle in the simulation
///
/// Each particle has a three-dimensional position, velocity, and force vector,
/// along with a mass value used for computing acceleration.
struct Particle {
position: [f64; 3],
velocity: [f64; 3],
force: [f64; 3],
mass: f64,
}
/// Computes the Lennard-Jones potential between two particles
///
/// The Lennard-Jones potential is used to model interactions between a pair of neutral atoms or molecules.
/// It includes a term that represents the repulsive forces at short distances and an attractive term at longer distances.
///
/// # Arguments
///
/// * `p1` - A reference to the first particle.
/// * `p2` - A reference to the second particle.
///
/// # Returns
///
/// * A floating-point value representing the potential energy between the two particles.
fn lennard_jones_potential(p1: &Particle, p2: &Particle) -> f64 {
// Calculate the Euclidean distance between p1 and p2.
let mut distance_sq = 0.0;
for i in 0..3 {
distance_sq += (p1.position[i] - p2.position[i]).powi(2);
}
let distance = distance_sq.sqrt();
// Define parameters for the Lennard-Jones potential.
let sigma = 1.0;
let epsilon = 1.0;
// Compute the Lennard-Jones potential using the standard formula.
4.0 * epsilon * ((sigma / distance).powi(12) - (sigma / distance).powi(6))
}
/// Advances the simulation by one time step using the Velocity Verlet integration scheme.
///
/// This function updates the positions and velocities of all particles based on the forces acting on them.
/// It then resets the forces for the next iteration and computes new forces using the Lennard-Jones potential.
/// In a more complete simulation, the force computation would include contributions from other interactions.
///
/// # Arguments
///
/// * `particles` - A mutable slice of particles in the system.
/// * `dt` - The time step for the simulation.
fn time_step(particles: &mut [Particle], dt: f64) {
// Update positions based on current velocity and acceleration.
for p in particles.iter_mut() {
for i in 0..3 {
// Update velocity with current force divided by mass.
p.velocity[i] += (p.force[i] / p.mass) * dt;
// Update position based on the new velocity.
p.position[i] += p.velocity[i] * dt;
}
}
// Reset forces before recalculating them.
for p in particles.iter_mut() {
p.force = [0.0; 3];
}
// Compute forces due to the Lennard-Jones potential.
// In a complete simulation, the force on each particle is derived from the gradient of the potential.
// Here, we simply compute the potential as a placeholder.
for i in 0..particles.len() {
for j in i + 1..particles.len() {
let _potential = lennard_jones_potential(&particles[i], &particles[j]);
// In a full implementation, calculate the derivative of the potential with respect to position
// and update particles[i].force and particles[j].force accordingly.
}
}
}
fn main() {
// Initialize a small system of two particles with given positions, zero initial velocities, and unit mass.
let mut particles = vec![
Particle { position: [1.0, 0.0, 0.0], velocity: [0.0, 0.0, 0.0], force: [0.0; 3], mass: 1.0 },
Particle { position: [2.0, 0.0, 0.0], velocity: [0.0, 0.0, 0.0], force: [0.0; 3], mass: 1.0 },
];
// Define the time step for the simulation.
let dt = 0.01;
// Run the simulation for 1000 time steps.
for _ in 0..1000 {
time_step(&mut particles, dt);
println!("Particle 1: Position = {:?}", particles[0].position);
println!("Particle 2: Position = {:?}", particles[1].position);
}
}
This implementation demonstrates a simplified MD simulation where particles interact through a Lennard-Jones potential. The Particle structure encapsulates the state of each particle, and the lennard_jones_potential function computes the interaction energy based on interparticle distance. The time_step function uses a basic integration scheme to update positions and velocities while resetting forces in preparation for the next iteration. Although the force computation in this example is not fully implemented, the structure provides a framework that can be expanded to include detailed force calculations from various molecular interactions.
Protein folding is another significant application of MD simulations. A simulation can track the folding process of a protein as it transitions from an extended chain of atoms into a stable, functional three-dimensional structure. In realistic simulations, complex force fields such as AMBER or CHARMM are employed to accurately model interactions, including bond stretching, angle bending, and torsional forces. The following conceptual example outlines how a basic protein folding simulation might be structured in Rust:
/// Computes forces between atoms in a protein using the Lennard-Jones potential.
///
/// This function iterates over all pairs of atoms in the protein and calculates the interaction potential.
/// In an advanced simulation, the resulting force vectors would be used to update the positions and velocities
/// of the atoms to simulate the folding process.
///
/// # Arguments
///
/// * `protein` - A mutable slice representing the atoms of the protein.
fn compute_protein_forces(protein: &mut [Particle]) {
// Reset forces for all atoms in the protein.
for atom in protein.iter_mut() {
atom.force = [0.0; 3];
}
// Compute pairwise forces based on the Lennard-Jones potential.
for i in 0..protein.len() {
for j in i + 1..protein.len() {
let _potential = lennard_jones_potential(&protein[i], &protein[j]);
// In a complete implementation, compute the force vector from the potential and update:
// protein[i].force and protein[j].force accordingly.
}
}
}
fn main() {
// Initialize a simplified protein model as a chain of atoms.
let mut protein = vec![
Particle { position: [0.0, 0.0, 0.0], velocity: [0.0, 0.0, 0.0], force: [0.0; 3], mass: 1.0 },
Particle { position: [1.5, 0.0, 0.0], velocity: [0.0, 0.0, 0.0], force: [0.0; 3], mass: 1.0 },
// Additional atoms representing the protein chain would be added here.
];
// Set a smaller time step for higher resolution in protein folding simulation.
let dt = 0.001;
// Run the simulation for 10,000 time steps to capture folding dynamics.
for _ in 0..10000 {
compute_protein_forces(&mut protein);
time_step(&mut protein, dt);
}
// Output the final positions of the protein atoms.
for (i, atom) in protein.iter().enumerate() {
println!("Atom {}: Position = {:?}", i, atom.position);
}
}
In this protein folding simulation example, the function compute_protein_forces is used to calculate the interaction forces between atoms in a protein chain. Although simplified here, this framework can be extended to incorporate more sophisticated force fields and interactions. MD simulations like these are invaluable in drug design, where understanding protein-ligand interactions and conformational changes is key to predicting binding affinity and stability.
Rust’s efficiency and safety, along with its support for parallel processing, enable the execution of computationally intensive MD simulations with high performance and scalability. By leveraging Rust for molecular dynamics and structural biology applications, researchers gain a powerful platform for exploring the dynamic behavior of biomolecules under physiological conditions, ultimately advancing our understanding of complex biological processes.
46.6. Computational Genomics
Computational genomics is a pivotal field that focuses on analyzing and interpreting the vast amounts of data produced by genome sequencing technologies. This discipline applies computational methods to understand the structure, function, evolution, and mapping of genomes. With the advent of high-throughput sequencing techniques, such as next-generation sequencing (NGS), researchers are now capable of sequencing entire genomes in a matter of days, resulting in massive datasets that demand sophisticated computational approaches for accurate interpretation and analysis.
The core areas in computational genomics include genome assembly, variant calling, and functional annotation. Genome assembly involves reconstructing the original genome from numerous short sequence reads generated by modern sequencing platforms. This complex process must address challenges such as sequencing errors, repetitive regions, and gaps that may occur during read generation. Variant calling, on the other hand, focuses on identifying genetic differences—such as single nucleotide polymorphisms (SNPs) or structural variations—that distinguish one individual’s genome from another. These variants are critical for understanding genetic diversity, disease susceptibility, and evolutionary dynamics. Functional annotation involves identifying genes and other genomic elements and assigning biological roles to them, thereby providing deeper insight into their contributions to cellular processes.
The computational tools developed for genomics are crucial for processing enormous datasets and uncovering the genetic underpinnings of diseases, traits, and evolutionary changes. One major application is precision medicine, where the identification of genetic variants is used to tailor medical treatments to the genetic profile of individual patients. For instance, by analyzing the genomic data of cancer patients, researchers can pinpoint mutations that drive tumor growth and select targeted therapies to inhibit these specific alterations.
Computational genomics also plays an essential role in gene therapy, where a comprehensive understanding of an individual’s genome is necessary for designing treatments that can correct or replace defective genes. Efficient analysis of large genomic datasets is fundamental for the success of these therapeutic strategies, and there is a growing demand for tools that can process such data quickly and accurately.
Rust’s performance and memory safety features make it an excellent language for implementing algorithms in computational genomics, especially when handling large-scale genomic datasets. The examples below demonstrate how to implement two essential techniques in computational genomics: genome assembly using a de Bruijn graph approach and variant detection through SNP identification.
use std::collections::HashMap;
/// Generates all possible k-mers (subsequences of length k) from a given sequence.
///
/// This function iterates over the input sequence and extracts every contiguous subsequence
/// of length k, storing each k-mer as a String in a vector.
///
/// # Arguments
///
/// * `sequence` - A string slice representing the genomic sequence.
/// * `k` - The length of each k-mer to be generated.
///
/// # Returns
///
/// * A vector containing all k-mers extracted from the sequence.
fn generate_kmers(sequence: &str, k: usize) -> Vec<String> {
let seq_len = sequence.len();
let mut kmers = Vec::new();
if seq_len < k {
return kmers;
}
for i in 0..=seq_len - k {
kmers.push(sequence[i..i + k].to_string());
}
kmers
}
/// Constructs a de Bruijn graph from a collection of k-mers.
///
/// The de Bruijn graph is represented as a HashMap where each key is a k-mer prefix (all but
/// the last character) and the corresponding value is a vector of suffixes (all but the first character)
/// that follow the prefix in the original k-mers.
///
/// # Arguments
///
/// * `kmers` - A vector of Strings containing the k-mers.
///
/// # Returns
///
/// * A HashMap representing the de Bruijn graph.
fn build_de_bruijn_graph(kmers: Vec<String>) -> HashMap<String, Vec<String>> {
let mut graph: HashMap<String, Vec<String>> = HashMap::new();
for kmer in kmers {
if kmer.len() < 2 {
continue;
}
let prefix = kmer[..kmer.len() - 1].to_string();
let suffix = kmer[1..].to_string();
graph.entry(prefix).or_insert_with(Vec::new).push(suffix);
}
graph
}
/// Assembles a genome sequence by traversing a de Bruijn graph.
///
/// Starting from an arbitrary node in the graph, this function follows the edges by selecting the
/// first available suffix at each step, appending the last character of each suffix to the assembled genome.
/// This simplified approach demonstrates the concept of genome assembly using de Bruijn graphs.
///
/// # Arguments
///
/// * `graph` - A de Bruijn graph represented as a HashMap.
///
/// # Returns
///
/// * A String representing the assembled genome.
fn assemble_genome(graph: HashMap<String, Vec<String>>) -> String {
let mut assembled_genome = String::new();
// Start from an arbitrary node in the graph.
let mut current_kmer = graph.keys().next().unwrap().to_string();
assembled_genome.push_str(¤t_kmer);
// Traverse the graph until no further extensions are available.
while let Some(suffixes) = graph.get(¤t_kmer) {
if suffixes.is_empty() {
break;
}
// Select the first available suffix.
let next_kmer = &suffixes[0];
// Append the last character of the next k-mer to the assembled genome.
assembled_genome.push(next_kmer.chars().last().unwrap());
current_kmer = next_kmer.clone();
}
assembled_genome
}
fn main() {
// Example sequence to be assembled.
let sequence = "ACGTACGTGACG";
let k = 4;
// Generate k-mers from the sequence.
let kmers = generate_kmers(sequence, k);
// Build the de Bruijn graph from the generated k-mers.
let de_bruijn_graph = build_de_bruijn_graph(kmers);
// Assemble the genome by traversing the de Bruijn graph.
let assembled_genome = assemble_genome(de_bruijn_graph);
println!("Assembled genome: {}", assembled_genome);
}
In this example, the genome assembly process is demonstrated using a de Bruijn graph approach. The function generate_kmers breaks the input sequence into overlapping k-mers. The build_de_bruijn_graph function then constructs a graph where each node corresponds to a prefix of a k-mer and edges represent the possible extensions of that prefix. Finally, the assemble_genome function traverses the graph to reconstruct the genome sequence by following overlaps between k-mers. In real-world applications, the de Bruijn graph approach is applied to far larger datasets, and more sophisticated methods are used to resolve ambiguities.
Variant detection is another critical task in computational genomics, aimed at identifying genetic differences between sequences. The following Rust code demonstrates a simple approach to detect single nucleotide polymorphisms (SNPs) by comparing two sequences.
/// Detects single nucleotide polymorphisms (SNPs) between two genomic sequences.
///
/// This function compares two sequences character by character up to the length of the shorter sequence.
/// When a difference is found, the function records the position along with the differing nucleotides.
///
/// # Arguments
///
/// * `seq1` - A string slice representing the first genomic sequence.
/// * `seq2` - A string slice representing the second genomic sequence.
///
/// # Returns
///
/// * A vector of tuples, each containing the position of the SNP and the corresponding nucleotides from both sequences.
fn detect_snps(seq1: &str, seq2: &str) -> Vec<(usize, char, char)> {
let length = seq1.len().min(seq2.len());
let mut snps = Vec::new();
for i in 0..length {
let base1 = seq1.chars().nth(i).unwrap();
let base2 = seq2.chars().nth(i).unwrap();
if base1 != base2 {
snps.push((i, base1, base2));
}
}
snps
}
fn main() {
// Define two genomic sequences to compare.
let sequence1 = "ACGTACGTGACG";
let sequence2 = "ACCTACGTGTCG";
// Detect SNPs between the sequences.
let snps = detect_snps(sequence1, sequence2);
// Print each detected SNP with its position and the differing bases.
for (pos, base1, base2) in snps {
println!("SNP detected at position {}: {} -> {}", pos, base1, base2);
}
}
This variant detection code defines the function detect_snps, which compares two sequences and identifies positions where the nucleotides differ, thereby detecting SNPs. Although this implementation is simple, it illustrates the fundamental concept behind more advanced variant detection pipelines. In practice, variant detection involves additional steps such as aligning sequencing reads to a reference genome and applying probabilistic models to account for sequencing errors.
Processing large genomic datasets presents significant challenges in terms of computational speed and memory usage. Rust’s memory safety guarantees, provided by its ownership model, help prevent common issues like memory leaks and segmentation faults. Moreover, Rust’s ability to handle parallel processing allows developers to build multi-threaded solutions that efficiently process massive amounts of data. By leveraging Rust for computational genomics, researchers can construct highly efficient and scalable pipelines for genome assembly, variant detection, and functional annotation. These tools are essential for advancing our understanding of the genetic basis of diseases, traits, and evolutionary processes, and they pave the way for breakthroughs in precision medicine, gene therapy, and evolutionary biology.
46.7. Computational Neuroscience
Computational neuroscience is the discipline that applies mathematical models and computational techniques to elucidate the functioning of the nervous system. This field plays a crucial role in unraveling the complexity of the brain, providing insights into how it processes information, regulates behavior, and supports higher cognitive functions. Computational models serve as virtual laboratories that enable neuroscientists to simulate the electrical activity of neurons, the dynamics of neural circuits, and even the behavior of entire brain networks, thereby offering a window into the inner workings of the brain.
Neural modeling, synaptic dynamics, and brain connectivity are central themes in computational neuroscience. Neural models provide mathematical representations of neurons, describing the mechanisms by which they receive, process, and transmit signals. Synaptic dynamics characterize how the strength of synaptic connections changes over time, a phenomenon that is essential for learning and memory. Brain connectivity models map out the structural and functional links between different brain regions, revealing how large-scale networks collaborate to produce behavior and cognition.
Computational models are indispensable for testing hypotheses about brain function and cognitive processes. For instance, simulations of neural circuits help to explain how networks of neurons give rise to complex behaviors such as decision-making, motor control, and sensory processing. These models are also critical for exploring cognitive processes like learning and memory, where synaptic plasticity—the adjustment of synaptic strength based on neuronal activity—plays a key role. By simulating neural circuits, researchers can study the mechanisms behind memory encoding and retrieval, investigate the flow of information across neural networks, and gain insights into the disruptions that underlie neurological disorders.
Rust’s performance, memory safety, and support for concurrent programming make it an ideal language for implementing detailed neural models and large-scale brain simulations. The following examples demonstrate how to model neuron dynamics using two well-known approaches: the Hodgkin-Huxley model and the integrate-and-fire model.
use std::f64::consts::E;
/// Constants for ion channels and membrane properties
const G_NA: f64 = 120.0; // Maximum sodium conductance
const G_K: f64 = 36.0; // Maximum potassium conductance
const G_L: f64 = 0.3; // Leak conductance
const E_NA: f64 = 50.0; // Sodium reversal potential
const E_K: f64 = -77.0; // Potassium reversal potential
const E_L: f64 = -54.387; // Leak reversal potential
const C_M: f64 = 1.0; // Membrane capacitance
/// Implements a simplified version of the Hodgkin-Huxley model for neuron dynamics.
///
/// This function computes the updates for the membrane voltage and the gating variables (m, h, n)
/// based on the Hodgkin-Huxley equations. It calculates the rate constants for each gating variable,
/// computes the ionic currents from sodium, potassium, and leak channels, and then updates the state
/// variables using Euler integration.
///
/// # Arguments
///
/// * `voltage` - Current membrane potential in mV.
/// * `m` - Current value of the sodium activation gating variable.
/// * `h` - Current value of the sodium inactivation gating variable.
/// * `n` - Current value of the potassium activation gating variable.
/// * `dt` - Time step for the integration.
/// * `I_ext` - External current injected into the neuron.
///
/// # Returns
///
/// * A tuple containing the updated membrane voltage, m, h, and n values.
fn hodgkin_huxley(voltage: f64, m: f64, h: f64, n: f64, dt: f64, I_ext: f64) -> (f64, f64, f64, f64) {
// Calculate gating variable rate constants for sodium activation (m)
let alpha_m = (0.1 * (25.0 - voltage)) / ((25.0 - voltage).exp() - 1.0);
let beta_m = 4.0 * (-voltage / 18.0).exp();
// Calculate gating variable rate constants for sodium inactivation (h)
let alpha_h = 0.07 * (-voltage / 20.0).exp();
let beta_h = 1.0 / ((30.0 - voltage).exp() + 1.0);
// Calculate gating variable rate constants for potassium activation (n)
let alpha_n = (0.01 * (10.0 - voltage)) / ((10.0 - voltage).exp() - 1.0);
let beta_n = 0.125 * (-voltage / 80.0).exp();
// Compute the derivatives of the gating variables
let dm_dt = alpha_m * (1.0 - m) - beta_m * m;
let dh_dt = alpha_h * (1.0 - h) - beta_h * h;
let dn_dt = alpha_n * (1.0 - n) - beta_n * n;
// Compute conductances based on the gating variables
let g_na = G_NA * m.powi(3) * h;
let g_k = G_K * n.powi(4);
let g_l = G_L;
// Compute ionic currents for sodium, potassium, and leak channels
let I_na = g_na * (voltage - E_NA);
let I_k = g_k * (voltage - E_K);
let I_l = g_l * (voltage - E_L);
// Compute the rate of change of the membrane potential using current balance equation
let dV_dt = (I_ext - I_na - I_k - I_l) / C_M;
// Update the state variables using Euler integration
(
voltage + dV_dt * dt,
m + dm_dt * dt,
h + dh_dt * dt,
n + dn_dt * dt,
)
}
fn main() {
// Initialize membrane potential and gating variables for the neuron.
let mut voltage = -65.0;
let mut m = 0.05;
let mut h = 0.6;
let mut n = 0.32;
// Set the integration time step and external current.
let dt = 0.01;
let I_ext = 10.0; // External current injected into the neuron
// Run the simulation for 1000 time steps.
for _ in 0..1000 {
let (new_voltage, new_m, new_h, new_n) = hodgkin_huxley(voltage, m, h, n, dt, I_ext);
voltage = new_voltage;
m = new_m;
h = new_h;
n = new_n;
println!("Voltage: {:.2} mV", voltage);
}
}
In this implementation of the Hodgkin-Huxley model, the neuron’s membrane potential and the gating variables m, h, and n are updated at each time step based on ionic currents and channel dynamics. The numerical integration is performed using Euler’s method, and the model simulates the initiation and propagation of action potentials in response to an external current.
A simpler yet widely used model in computational neuroscience is the integrate-and-fire model, which abstracts the neuron's behavior into a process of integrating incoming current until a threshold is reached, triggering an action potential and resetting the membrane potential. The following example illustrates a basic integrate-and-fire neuron model.
/// Implements the integrate-and-fire model for neuron spiking.
///
/// This function updates the membrane potential of a neuron by integrating the input current.
/// If the membrane potential reaches or exceeds a specified threshold, the neuron is considered to have fired,
/// and the potential is reset.
///
/// # Arguments
///
/// * `voltage` - Current membrane potential in mV.
/// * `I_ext` - External current input.
/// * `dt` - Time step for the integration.
/// * `threshold` - Membrane potential threshold for triggering a spike.
///
/// # Returns
///
/// * A tuple containing the updated membrane potential and a boolean indicating whether the neuron fired.
fn integrate_and_fire(voltage: f64, I_ext: f64, dt: f64, threshold: f64) -> (f64, bool) {
let tau_m = 20.0; // Membrane time constant in ms
// Compute the rate of change of the membrane potential
let dV_dt = (I_ext - voltage) / tau_m;
let new_voltage = voltage + dV_dt * dt;
// Check if the new membrane potential exceeds the threshold
if new_voltage >= threshold {
(0.0, true) // Reset voltage after firing
} else {
(new_voltage, false)
}
}
fn main() {
// Initialize the membrane potential for the integrate-and-fire model.
let mut voltage = -65.0;
let threshold = -50.0; // Spike threshold in mV
let dt = 0.1;
let I_ext = 15.0; // External current input
// Simulate the neuron for 100 time steps.
for _ in 0..100 {
let (new_voltage, fired) = integrate_and_fire(voltage, I_ext, dt, threshold);
voltage = new_voltage;
if fired {
println!("Neuron fired!");
} else {
println!("Voltage: {:.2} mV", voltage);
}
}
}
In the integrate-and-fire model example, the function integrate_and_fire simulates the neuron's behavior by integrating the input current over time. When the membrane potential reaches the threshold value, the neuron fires and the voltage is reset, mimicking the spiking behavior observed in biological neurons.
Synaptic plasticity, which refers to the activity-dependent adjustment of synaptic strengths, is another vital component in computational neuroscience. Models such as Spike-Timing-Dependent Plasticity (STDP) can be implemented in Rust to simulate learning processes at the synaptic level. By modifying synaptic weights based on the precise timing of pre- and post-synaptic spikes, these models help to elucidate how neural circuits adapt and reorganize in response to stimuli.
Large-scale brain network analysis involves modeling neurons as nodes and synaptic connections as edges, which allows researchers to investigate connectivity patterns and network dynamics across extensive neural circuits. Rust’s ability to handle concurrency is particularly advantageous in this context, as different regions of the network can be simulated in parallel, significantly enhancing computational efficiency.
Rust’s performance, safety, and concurrency features empower computational neuroscientists to build scalable, efficient models of neural dynamics, synaptic plasticity, and brain connectivity. These models provide invaluable insights into the mechanisms underlying cognition, learning, and neural disorders, advancing our understanding of the brain and opening new avenues for therapeutic interventions.
46.8. Drug Discovery and Virtual Screening
Drug discovery is a complex and resource-intensive endeavor that traditionally relied on extensive wet-lab high-throughput screening of chemical compounds to identify those capable of interacting with biological targets. With rapid advances in computational power and algorithms, in silico methods have revolutionized the field by enabling faster and more cost-effective identification of promising drug candidates. Virtual screening, molecular docking, and pharmacophore modeling have become essential computational approaches that simulate the interactions between potential drugs (ligands) and their biological targets (receptors), thereby accelerating the discovery process.
Virtual screening employs sophisticated computational tools to sift through vast libraries of compounds and predict their binding affinities to a target protein, narrowing down a large pool of molecules to a manageable number of candidates. Molecular docking builds on this by simulating the physical fit of a small molecule into the active site of a target protein, evaluating the binding efficiency based on spatial complementarity and interaction energies. Pharmacophore modeling, on the other hand, focuses on identifying the key chemical features necessary for molecular recognition, aiding in the rational design of new drugs that possess the essential characteristics required for effective target engagement.
The computational methods used in drug discovery are indispensable for early-stage identification and optimization of potential therapeutics. By simulating ligand-receptor interactions at an atomic level, these approaches not only predict the efficacy of drug candidates but also provide insights into their potential toxicity and side effects. This predictive capability allows researchers to eliminate unsuitable candidates early in the development pipeline, thereby conserving resources and reducing the likelihood of late-stage failures. In the pharmaceutical industry, computational drug design is instrumental for tailoring therapies that target specific proteins or pathways involved in disease processes. For instance, detailed molecular docking studies can reveal how a candidate drug binds to a mutated protein associated with cancer, allowing for the optimization of its chemical structure to enhance efficacy and minimize adverse effects.
Rust's performance, memory safety, and concurrency features make it an excellent choice for implementing drug discovery algorithms, especially when processing large libraries of compounds. The following example demonstrates a simplified ligand-receptor docking model implemented in Rust. In this model, the interaction between a ligand (drug candidate) and a receptor (protein target) is simulated by computing the binding energy based on the distances between atoms in the two molecules. This approach is analogous to molecular docking, where the potential energy of the interaction provides a measure of binding affinity.
use std::f64::consts::PI;
/// Represents an atom in a ligand or receptor with its 3D coordinates.
struct Atom {
x: f64,
y: f64,
z: f64,
}
/// Computes the Euclidean distance between two atoms.
///
/// This function calculates the straight-line distance in three-dimensional space,
/// which is essential for determining how closely two atoms approach each other.
///
/// # Arguments
///
/// * `atom1` - A reference to the first atom.
/// * `atom2` - A reference to the second atom.
///
/// # Returns
///
/// * The distance between the two atoms as a floating-point number.
fn distance(atom1: &Atom, atom2: &Atom) -> f64 {
((atom1.x - atom2.x).powi(2) +
(atom1.y - atom2.y).powi(2) +
(atom1.z - atom2.z).powi(2)).sqrt()
}
/// Computes the binding energy between two atoms based on a simplified Lennard-Jones potential.
///
/// The Lennard-Jones potential provides a simple model for atomic interactions,
/// capturing both repulsive and attractive forces as a function of distance.
///
/// # Arguments
///
/// * `dist` - The distance between two atoms.
///
/// # Returns
///
/// * The computed binding energy as a floating-point number.
fn binding_energy(dist: f64) -> f64 {
let sigma = 1.0;
let epsilon = 1.0;
// The potential comprises a repulsive term (sigma/distance)^12 and an attractive term (sigma/distance)^6.
4.0 * epsilon * ((sigma / dist).powi(12) - (sigma / dist).powi(6))
}
/// Simulates the ligand-receptor docking process by calculating the total binding energy.
///
/// This function iterates over all atoms in the ligand and receptor, computes the distance
/// between each pair of atoms, and accumulates the corresponding binding energies using
/// a simplified Lennard-Jones potential. The total binding energy provides an estimate of
/// the binding affinity between the ligand and receptor.
///
/// # Arguments
///
/// * `ligand` - A slice of Atom structures representing the ligand.
/// * `receptor` - A slice of Atom structures representing the receptor.
///
/// # Returns
///
/// * The total binding energy as a floating-point number.
fn ligand_receptor_docking(ligand: &[Atom], receptor: &[Atom]) -> f64 {
let mut total_energy = 0.0;
// Iterate over each atom in the ligand.
for ligand_atom in ligand {
// For each ligand atom, iterate over each atom in the receptor.
for receptor_atom in receptor {
let dist = distance(ligand_atom, receptor_atom);
// Ensure that the distance is non-zero to avoid division by zero errors.
if dist > 0.0 {
total_energy += binding_energy(dist);
}
}
}
total_energy
}
fn main() {
// Define a simplified ligand as a set of atoms with 3D coordinates.
let ligand = vec![
Atom { x: 0.0, y: 0.0, z: 0.0 },
Atom { x: 1.0, y: 1.0, z: 1.0 },
];
// Define a simplified receptor as a set of atoms with 3D coordinates.
let receptor = vec![
Atom { x: 5.0, y: 5.0, z: 5.0 },
Atom { x: 6.0, y: 6.0, z: 6.0 },
];
// Compute the total binding energy for the ligand-receptor interaction.
let total_energy = ligand_receptor_docking(&ligand, &receptor);
println!("Total binding energy: {:.4}", total_energy);
}
In this implementation, the Atom struct encapsulates the three-dimensional coordinates of an atom. The distance function calculates the Euclidean distance between any two atoms, which is then used by the binding_energy function to compute a simplified interaction energy based on the Lennard-Jones potential. The ligand_receptor_docking function simulates the docking process by iterating through every pair of atoms—one from the ligand and one from the receptor—and summing their binding energies to obtain a total score. This score provides an estimate of the ligand’s binding affinity to the receptor.
In real-world applications, molecular docking simulations incorporate more sophisticated scoring functions that account for additional factors such as electrostatics, hydrogen bonding, and solvation effects. Once a promising docking pose is identified, further simulations, including molecular dynamics, can be performed to evaluate the stability of the ligand-receptor complex over time. Moreover, pharmacokinetic models can be implemented to predict how the drug candidate will be absorbed, distributed, metabolized, and excreted (ADME) in the human body.
In large-scale drug discovery projects, Rust can be leveraged to build high-throughput virtual screening pipelines. Such pipelines typically involve importing extensive chemical libraries, performing initial docking simulations to calculate binding energies for thousands of compounds in parallel, ranking these compounds based on their predicted affinities, and then refining the top candidates with more detailed simulations. Rust’s concurrency features allow these processes to be executed concurrently, dramatically speeding up the screening process while ensuring memory safety and reliability.
By utilizing Rust for computational drug discovery, researchers can develop robust, scalable pipelines that process vast datasets with high precision and speed. This integration of advanced computational methods into the drug discovery process holds significant promise for accelerating the identification of novel therapeutics and advancing personalized medicine initiatives.
46.9. Case Studies and Applications
Computational biology has far-reaching applications across medicine, agriculture, and biotechnology. The capacity to model complex biological systems through computational techniques enables researchers to address real-world challenges such as identifying disease biomarkers, developing novel therapeutic drugs, and improving crop yields through advanced genomics. The ever-growing availability of biological data, together with rapid advancements in computational methods, has made it possible to simulate, analyze, and predict biological phenomena at scales previously unimaginable.
In medicine, computational models are employed to identify disease biomarkers, which are molecular indicators associated with the onset or progression of diseases. By analyzing gene expression data, for instance, researchers can pinpoint specific genes or proteins that serve as reliable indicators for conditions like cancer or cardiovascular disorders. In agriculture, genomics plays a transformative role in crop improvement by revealing genetic variants that enhance traits such as yield, drought tolerance, and pest resistance, thereby informing more effective plant breeding strategies. Biotechnology applications extend these capabilities further, including the design of synthetic organisms engineered to produce valuable compounds such as biofuels or pharmaceuticals.
Numerous case studies illustrate the significant impact of computational biology across these domains. One prominent example involves the identification of disease biomarkers through the analysis of high-throughput genomic and proteomic data. These biomarkers not only serve as critical tools for early diagnosis but also enable personalized medicine approaches, where treatments are tailored to an individual’s genetic profile. In the realm of drug development, computational models facilitate the prediction of drug-target interactions, accelerating the design of new therapies by anticipating both efficacy and potential side effects.
In agriculture, computational genomics has revolutionized crop improvement by enabling researchers to sift through extensive genomic datasets to identify genes associated with beneficial traits. This knowledge supports the creation of more resilient and productive crops, addressing global food security challenges. The power of computational biology is further underscored by its applications in biotechnology, where in silico methods aid in the design of novel compounds and the engineering of organisms for industrial purposes.
Rust offers numerous advantages for computational biology with its high performance and memory safety features, making it well-suited for implementing large-scale biological models and data analysis pipelines. The following examples demonstrate practical applications of Rust in real-world computational biology.
Example 1: Disease Biomarker Identification Using Gene Expression Data
Gene expression data is pivotal for identifying disease biomarkers. Rust can be used to efficiently process large datasets, such as RNA sequencing data, to uncover genes that exhibit significant differential expression between healthy and diseased samples. In the example below, the fold change and p-value are calculated as preliminary indicators of differential expression.
use ndarray::Array1;
use ndarray_stats::QuantileExt;
/// Calculates the fold change between healthy and diseased gene expression samples.
///
/// The fold change is computed as the ratio of the mean expression in diseased samples to that in healthy samples.
///
/// # Arguments
///
/// * `healthy` - An Array1<f64> representing gene expression values in healthy samples.
/// * `diseased` - An Array1<f64> representing gene expression values in diseased samples.
///
/// # Returns
///
/// * A floating-point value representing the fold change.
fn fold_change(healthy: &Array1<f64>, diseased: &Array1<f64>) -> f64 {
let mean_healthy = healthy.mean().unwrap();
let mean_diseased = diseased.mean().unwrap();
mean_diseased / mean_healthy
}
/// Calculates a simplified p-value for differential expression based on a t-test statistic.
///
/// This function uses a placeholder t-test function to obtain a t-statistic and then computes a dummy cumulative
/// distribution function value. In a full implementation, a robust statistical test with multiple testing correction
/// would be applied.
///
/// # Arguments
///
/// * `healthy` - An Array1<f64> of expression values for healthy samples.
/// * `diseased` - An Array1<f64> of expression values for diseased samples.
///
/// # Returns
///
/// * A floating-point p-value representing the significance of the difference.
fn p_value(healthy: &Array1<f64>, diseased: &Array1<f64>) -> f64 {
let t_statistic = t_test(healthy, diseased);
// A dummy cumulative distribution function call for demonstration.
1.0 - t_statistic / 10.0 // Simplified p-value calculation
}
/// Placeholder function for performing a t-test on two sample arrays.
///
/// In a full implementation, this function would compute the t-statistic comparing the two groups.
///
/// # Arguments
///
/// * `_healthy` - Expression values for healthy samples.
/// * `_diseased` - Expression values for diseased samples.
///
/// # Returns
///
/// * A dummy t-statistic value.
fn t_test(_healthy: &Array1<f64>, _diseased: &Array1<f64>) -> f64 {
2.0 // Dummy value representing a t-statistic
}
fn main() {
// Example gene expression data for healthy and diseased samples.
let healthy_samples = Array1::from(vec![12.0, 15.0, 13.5, 14.8, 15.2]);
let diseased_samples = Array1::from(vec![20.0, 22.0, 21.5, 19.8, 23.2]);
// Calculate fold change and p-value to assess differential expression.
let fold_change_value = fold_change(&healthy_samples, &diseased_samples);
let p_val = p_value(&healthy_samples, &diseased_samples);
println!("Fold change: {:.2}", fold_change_value);
println!("P-value: {:.4}", p_val);
}
In this example, the fold_change function computes the ratio of mean expression levels between diseased and healthy samples, and the p_value function returns a simplified measure of statistical significance. Libraries such as ndarray facilitate numerical computations, ensuring that even large datasets can be processed efficiently.
Example 2: Agricultural Genomics for Crop Improvement
In agricultural genomics, computational tools are used to identify genetic variants associated with desirable traits in crops, such as increased yield or pest resistance. The following Rust code demonstrates a basic genome-wide association study (GWAS) simulation, where SNP data is generated and then analyzed for its correlation with a trait of interest.
use ndarray::Array1;
use rand::Rng;
/// Simulates SNP data for a population of crops.
///
/// Each SNP is represented as an Array1<u8> where the values are in the range [0, 3],
/// representing different genotypes. This function generates a vector of such SNP arrays,
/// with each array corresponding to one SNP across multiple samples.
///
/// # Arguments
///
/// * `num_snps` - The number of SNPs to simulate.
/// * `num_samples` - The number of samples (individual crops) in the population.
///
/// # Returns
///
/// * A vector containing Array1<u8> instances representing SNP data.
fn simulate_snp_data(num_snps: usize, num_samples: usize) -> Vec<Array1<u8>> {
let mut rng = rand::thread_rng();
(0..num_snps)
.map(|_| {
let data: Vec<u8> = (0..num_samples)
.map(|_| rng.gen_range(0..3))
.collect();
Array1::from(data)
})
.collect()
}
/// Computes a simple genome-wide association study (GWAS) by calculating the correlation between SNP data and a trait.
///
/// This function iterates through each SNP in the dataset and computes a dummy correlation value with the trait values.
/// In a complete implementation, more sophisticated statistical methods would be used.
///
/// # Arguments
///
/// * `snps` - A slice of Array1<u8> representing SNP data for multiple SNPs.
/// * `trait_values` - An Array1<f64> representing the trait values for the corresponding samples.
///
/// # Returns
///
/// * A vector of correlation values for each SNP.
fn compute_gwas(snps: &[Array1<u8>], trait_values: &Array1<f64>) -> Vec<f64> {
snps.iter()
.map(|snp| {
let correlation = compute_correlation(snp, trait_values);
correlation
})
.collect()
}
/// Placeholder function for computing the correlation between a SNP and trait values.
///
/// In a full implementation, this would calculate a statistical correlation coefficient.
///
/// # Arguments
///
/// * `_snp` - SNP data for a single SNP.
/// * `_trait_values` - Trait values for the samples.
///
/// # Returns
///
/// * A dummy correlation value.
fn compute_correlation(_snp: &Array1<u8>, _trait_values: &Array1<f64>) -> f64 {
0.8 // Dummy correlation value
}
fn main() {
let num_snps = 100;
let num_samples = 50;
// Simulate SNP data for a population of crops.
let snps = simulate_snp_data(num_snps, num_samples);
// Example trait values representing a phenotype such as yield.
let trait_values = Array1::from(vec![5.0, 5.5, 6.0, 5.8, 6.2, 5.7, 6.1, 5.9, 6.3, 6.0, 5.8, 6.2, 5.9, 6.0, 6.1,
5.7, 6.3, 6.0, 5.8, 6.2, 5.9, 6.0, 6.1, 5.7, 6.3, 6.0, 5.8, 6.2, 5.9, 6.0,
6.1, 5.7, 6.3, 6.0, 5.8, 6.2, 5.9, 6.0, 6.1, 5.7, 6.3, 6.0, 5.8, 6.2, 5.9, 6.0,
6.1, 5.7, 6.3, 6.0]); // Extended for demonstration
// Compute GWAS results by correlating each SNP with the trait values.
let gwas_results = compute_gwas(&snps, &trait_values);
for (i, result) in gwas_results.iter().enumerate() {
println!("SNP {}: Correlation with trait: {:.2}", i, result);
}
}
In this second example, the simulate_snp_data function creates synthetic SNP data for a set of crop samples, while compute_gwas evaluates the association between each SNP and a trait of interest using a placeholder correlation function. In practical scenarios, these computations would involve rigorous statistical tests and corrections to account for multiple comparisons, especially when analyzing millions of genetic variants.
Rust’s efficient memory management, zero-cost abstractions, and powerful concurrency model make it exceptionally well-suited for processing and analyzing large biological datasets. Whether identifying disease biomarkers in human medicine or uncovering genetic variants for crop improvement, Rust enables the development of robust, scalable computational biology pipelines that can handle the immense data volumes generated by modern sequencing technologies.
The application of Rust in real-world computational biology—from disease diagnostics to agricultural genomics—demonstrates its versatility and capability in addressing complex biological challenges with speed, precision, and reliability. These case studies underscore the transformative potential of integrating advanced computational methods into biological research and biotechnology, paving the way for innovative solutions in personalized medicine, sustainable agriculture, and beyond.
46.10. Conclusion
Chapter 46 of CPVR equips readers with the knowledge and skills to apply computational techniques to biological research using Rust. By exploring the intersection of biology and computational physics, this chapter provides a robust framework for understanding and modeling complex biological systems. Through hands-on examples and real-world applications, readers are encouraged to leverage computational tools to drive innovation in the life sciences.
46.10.1. Further Learning with GenAI
The following prompts are designed to help learners explore the complexities of computational biology using Rust. These prompts focus on fundamental concepts, mathematical models, computational techniques, and practical applications related to computational biology.\ In what ways does the interdisciplinary integration of biology, computer science, mathematics, and data science drive the development and optimization of computational models in biological research? How do these disciplines uniquely contribute to advancing techniques such as genomic analysis, molecular simulations, and systems biology modeling? What are the current challenges in harmonizing these fields, and how can cross-disciplinary approaches be better leveraged to address complex biological questions?
How do deterministic models, such as ordinary differential equations, and stochastic models, like Markov processes and stochastic differential equations, differ in their capacity to simulate biological systems? What biological processes, such as gene expression, metabolic pathways, or ecological dynamics, are better suited to deterministic approaches versus stochastic ones? How can hybrid models be developed to capture both the precision of deterministic frameworks and the variability inherent in biological systems?
How do sequence alignment algorithms, including global alignment techniques like Needleman-Wunsch and local alignment methods like Smith-Waterman, facilitate the comparison of biological sequences? What advancements in heuristic algorithms like BLAST have improved the efficiency of large-scale genomic searches? What are the key computational, algorithmic, and biological challenges in scaling these techniques to analyze massive genomic datasets, particularly in terms of data storage, parallel computation, and error correction?
How do network models, including those modeling metabolic pathways, gene regulatory networks, and protein-protein interactions, provide insights into the complex, emergent properties of biological systems? How do these models help in understanding dynamic behaviors such as homeostasis, robustness, and adaptation in living organisms? What are the key computational challenges in modeling high-dimensional biological networks, and how can computational power, data availability, and model accuracy be balanced to improve our understanding of complex biological systems?
How do molecular dynamics (MD) simulations enable the detailed study of atomic-scale interactions and movements within biological macromolecules such as proteins, nucleic acids, and membranes? How do MD simulations contribute to understanding key biological processes like protein folding, ligand binding, and membrane transport? What are the major computational hurdles—such as scaling to large systems, long time-scale simulations, and force field accuracy—that must be addressed to make MD simulations more accessible and reliable for complex biological systems?
How do genome assembly algorithms, variant calling pipelines, and functional annotation tools collaborate to enable the large-scale analysis and interpretation of genomic data? What are the computational bottlenecks in assembling complex genomes, especially in handling repetitive sequences, structural variants, and sequencing errors? How can Rust be applied to improve the efficiency, scalability, and accuracy of computational pipelines for genomics, and what role do parallel computing and memory management play in these optimizations?
How do computational models of neuron dynamics, such as the Hodgkin-Huxley model and integrate-and-fire frameworks, enhance our understanding of individual neuron activity, synaptic transmission, and neural plasticity? How do models of synaptic plasticity and large-scale brain networks contribute to the study of brain function, learning, and cognition? What are the challenges in simulating the intricate connectivity of the brain at various scales, from individual neurons to whole-brain networks, and how can computational tools in Rust support the development of high-performance neural simulations?
How do in silico methods, including virtual screening, molecular docking, and pharmacophore modeling, accelerate the drug discovery process and enhance the prediction of drug-target interactions? What are the limitations and challenges in predicting binding affinity, specificity, and potential off-target effects using computational approaches? How can Rust’s performance and memory safety features contribute to the development of more scalable and efficient computational pipelines for virtual screening and molecular docking?
How do computational techniques manage the integration of heterogeneous biological data, including genomic, proteomic, transcriptomic, and clinical data, to develop accurate models of biological systems? What challenges arise from the complexity, volume, and noise present in biological datasets, and how can computational methods ensure data consistency, integration, and biological relevance? How can Rust’s data handling and parallelization capabilities be utilized to optimize data-intensive biological models for accuracy and performance?
How can Rust’s performance, concurrency, and memory safety features be leveraged to optimize computational simulations and data analysis tasks in computational biology? How do Rust’s unique capabilities—such as its ownership model, safe memory handling, and high-level abstractions—improve performance in biological research, particularly in high-performance applications like molecular dynamics simulations, genomic analysis, or systems biology modeling? What role does Rust play in ensuring both safety and speed when dealing with computationally intensive biological tasks?
How do computational models in systems biology offer insights into the emergent properties of biological systems, such as robustness, adaptability, and homeostasis? How do these models help in identifying how interactions at the molecular and cellular levels give rise to complex behaviors observed at the system level? What are the limitations of current systems biology models, and how can Rust-based implementations help address challenges related to the scalability and computational complexity of simulating large, interacting biological systems?
How do bioinformatics tools like sequence analysis, variant calling, and gene expression profiling enable the development of personalized medicine, tailored to individual genetic and molecular profiles? What challenges arise in integrating genomic, transcriptomic, and clinical data to create personalized treatment plans? How can Rust-based implementations improve the efficiency and scalability of bioinformatics tools, ensuring accurate and timely results for personalized medicine applications?
How do molecular docking algorithms predict the binding affinity and specificity between drug candidates and their molecular targets? What are the computational and algorithmic challenges in optimizing virtual screening pipelines to efficiently identify promising drug candidates from large compound libraries? How can Rust’s performance and safety features be applied to enhance the scalability and reliability of virtual screening and molecular docking processes in drug discovery?
How do computational genomics tools identify genetic variants associated with diseases, such as single-nucleotide polymorphisms (SNPs) and structural variants? What are the computational and biological challenges in interpreting large-scale genomic data, especially in the context of complex traits, gene-environment interactions, and polygenic disorders? How can Rust be employed to improve the computational efficiency and accuracy of variant detection and interpretation pipelines?
How do mathematical models of infectious disease dynamics simulate the spread of diseases within populations, predict the impact of public health interventions, and inform policy decisions? What are the strengths and limitations of different modeling approaches, such as SIR models, agent-based simulations, and network-based models, in capturing real-world disease dynamics? How can Rust-based implementations contribute to the efficiency, scalability, and accuracy of disease spread simulations, particularly in the context of pandemic preparedness?
How do machine learning algorithms contribute to the analysis of biological data, the prediction of complex biological outcomes, and the discovery of new biological insights? What challenges arise from the noisy, high-dimensional, and heterogeneous nature of biological datasets, and how can advanced machine learning techniques—such as deep learning, reinforcement learning, and transfer learning—be applied to extract meaningful patterns and predictions? How can Rust be used to develop efficient machine learning pipelines tailored to the needs of computational biology?
How do multiscale models integrate data and processes across different biological scales, from molecular interactions to cellular behaviors to tissue- and organism-level phenomena? What are the key challenges in developing and validating these models, particularly in terms of computational complexity, data integration, and cross-scale interactions? How can Rust be applied to improve the performance and scalability of multiscale biological simulations, enabling the study of complex, cross-scale biological processes?
How can Rust’s capabilities be leveraged to develop efficient and scalable computational tools for drug discovery, including virtual screening, molecular docking, and pharmacophore modeling? How do Rust’s concurrency and memory management features optimize high-performance computing tasks in drug discovery pipelines, ensuring both speed and safety in handling large datasets and complex calculations?
How do computational tools contribute to the improvement of agricultural processes, such as increasing crop yields, developing pest-resistant strains, and engineering genetically modified organisms? What are the specific challenges in applying computational models to large-scale agricultural systems, and how can Rust-based implementations improve the scalability, efficiency, and accuracy of agricultural simulations and data analysis?
How might Rust’s capabilities evolve to address emerging challenges in computational biology, such as the need for more scalable, high-performance simulations, or the integration of complex, multiscale data? What new opportunities could arise from advancements in Rust’s ecosystem and improvements in computational techniques, particularly in areas like personalized medicine, synthetic biology, and high-throughput genomic analysis? How can Rust-based computational tools help shape the future of biological research and innovation?
By engaging with these topics, you are building a strong foundation in computational biology and equipping yourself with the tools to contribute to cutting-edge research and innovation. Embrace the challenges, stay curious, and let your exploration of computational biology inspire you to push the boundaries of what is possible in this dynamic field.
46.10.2. Assignments for Practice
Each exercise offers an opportunity to explore the intersection of biology and computational biophysics, experiment with advanced simulations, and contribute to the development of new insights and technologies in the life sciences.
Exercise 46.1: Implementing Sequence Alignment Algorithms for DNA Analysis
Objective: Develop a Rust program to implement sequence alignment algorithms, such as Needleman-Wunsch and Smith-Waterman, for analyzing DNA sequences.
Steps:
Begin by researching the principles of sequence alignment and their application in bioinformatics. Write a brief summary explaining the significance of sequence alignment in identifying homologous sequences and understanding evolutionary relationships.
Implement a Rust program that performs sequence alignment using the Needleman-Wunsch and Smith-Waterman algorithms. Include options for global and local alignment, and visualize the aligned sequences.
Analyze the alignment results to identify conserved regions, mutations, and potential functional domains within the DNA sequences. Discuss the implications of these findings for understanding genetic variation and evolution.
Experiment with different scoring matrices, gap penalties, and alignment parameters to explore their impact on the alignment results. Write a report summarizing your findings and discussing the challenges in sequence alignment.
GenAI Support: Use GenAI to optimize the implementation of sequence alignment algorithms, troubleshoot issues in aligning large sequences, and interpret the results in the context of bioinformatics research.
Exercise 46.2: Modeling Gene Regulatory Networks Using Systems Biology Approaches
Objective: Implement a Rust-based simulation to model gene regulatory networks (GRNs) using systems biology approaches, focusing on the dynamics of gene expression.
Steps:
Study the principles of gene regulatory networks and their role in controlling gene expression. Write a brief explanation of how systems biology approaches model the interactions between genes, proteins, and other regulatory elements.
Implement a Rust program that simulates the dynamics of a gene regulatory network, including the transcriptional regulation, feedback loops, and signal transduction pathways. Focus on modeling the temporal changes in gene expression.
Analyze the simulation results to identify key regulatory genes, network motifs, and the effects of perturbations on gene expression. Visualize the dynamics of the GRN and discuss the implications for understanding cellular behavior.
Experiment with different network topologies, regulatory mechanisms, and environmental conditions to explore their impact on the GRN’s behavior. Write a report detailing your findings and discussing strategies for designing synthetic gene networks.
GenAI Support: Use GenAI to optimize the simulation of gene regulatory networks, troubleshoot issues in modeling complex interactions, and interpret the results in the context of systems biology.
Exercise 46.3: Simulating Protein Dynamics Using Molecular Dynamics (MD) Simulations
Objective: Develop a Rust-based program to simulate the dynamics of proteins using molecular dynamics (MD) simulations, focusing on protein folding and ligand-binding processes.
Steps:
Research the principles of molecular dynamics simulations and their application in studying protein dynamics. Write a brief summary explaining the significance of MD simulations in understanding protein structure and function.
Implement a Rust program that performs molecular dynamics simulations of a protein, including the calculation of forces, integration of equations of motion, and analysis of conformational changes.
Analyze the simulation results to identify key folding events, ligand-binding sites, and the effects of mutations on protein stability. Visualize the protein’s dynamics and discuss the implications for drug design and protein engineering.
Experiment with different force fields, temperature conditions, and simulation parameters to explore their impact on the protein’s behavior. Write a report summarizing your findings and discussing the challenges in simulating large biomolecular systems.
GenAI Support: Use GenAI to optimize the implementation of molecular dynamics simulations, troubleshoot issues in simulating protein dynamics, and interpret the results in the context of structural biology.
Exercise 46.4: Predicting Genetic Variants Using Computational Genomics Techniques
Objective: Implement a Rust-based simulation to predict genetic variants using computational genomics techniques, focusing on variant calling and functional annotation.
Steps:
Study the principles of variant calling and their application in identifying genetic variants from sequencing data. Write a brief explanation of how computational genomics techniques predict single nucleotide polymorphisms (SNPs) and other variants.
Implement a Rust program that performs variant calling on genomic data, including the detection of SNPs, insertions, deletions, and structural variants. Focus on analyzing the functional impact of the predicted variants.
Analyze the variant calling results to identify potential disease-associated variants, regulatory elements, and gene expression changes. Visualize the distribution of variants across the genome and discuss the implications for personalized medicine.
Experiment with different variant calling algorithms, filtering criteria, and annotation tools to explore their impact on the prediction results. Write a report detailing your findings and discussing strategies for improving variant detection accuracy.
GenAI Support: Use GenAI to optimize the variant calling pipeline, troubleshoot issues in analyzing large genomic datasets, and interpret the results in the context of computational genomics.
Exercise 46.5: Case Study - Designing Drug Candidates Using Virtual Screening and Molecular Docking
Objective: Apply computational methods to design drug candidates using virtual screening and molecular docking, focusing on identifying potential inhibitors for a target protein.
Steps:
Select a target protein and research its role in a specific disease. Write a summary explaining the significance of targeting this protein in drug discovery and the challenges in designing effective inhibitors.
Implement a Rust-based simulation to perform virtual screening of a compound library against the target protein, including the prediction of binding affinities and identification of top candidates for docking.
Perform molecular docking simulations to predict the binding modes of the top-ranked compounds, focusing on key interactions between the drug candidates and the target protein’s active site.
Analyze the docking results to identify potential drug candidates, assess their binding affinities, and predict their efficacy. Visualize the protein-ligand interactions and discuss the implications for drug design and optimization.
Experiment with different docking algorithms, scoring functions, and compound libraries to explore their impact on the screening and docking results. Write a detailed report summarizing your approach, the simulation results, and the implications for drug discovery.
GenAI Support: Use GenAI to guide the selection of compounds for virtual screening, optimize the docking simulations, and help interpret the results in the context of drug discovery.
Embrace the challenges, push the boundaries of your knowledge, and let your passion for computational biology drive you toward mastering the art of modeling complex biological systems. Your efforts today will lead to breakthroughs that shape the future of biology and medicine.
Comments