Chapter 14
Finite Element Analysis for Structural Mechanics
"Computational techniques, particularly in physics, open doors to understanding the most complex phenomena, turning equations into insights." — Steven Chu
Chapter 14 of CPVR delves into the powerful and versatile method of Finite Element Analysis (FEA) for structural mechanics, implemented using the Rust programming language. The chapter begins by laying a solid foundation in the mathematical principles that govern FEA, guiding the reader through discretization techniques, assembly of stiffness matrices, and the application of boundary conditions. As the reader progresses, they will explore various solver techniques, both direct and iterative, for solving the system of equations arising from FEA. The chapter also covers advanced topics such as nonlinear analysis and dynamic simulations, emphasizing the importance of performance optimization through parallel computing and efficient memory management in Rust. Practical implementation is at the heart of this chapter, with hands-on coding exercises, real-world case studies, and integration with visualization tools to ensure that readers not only understand the theory but also gain the skills to apply FEA to complex structural mechanics problems.
14.1. Introduction to Finite Element Analysis (FEA)
Finite Element Analysis (FEA) is a crucial computational tool in structural mechanics, used to solve complex problems that involve the behavior of materials and structures under various forces. It has a profound significance in modern engineering applications, enabling the analysis of structures that would be too complex to solve analytically. The evolution of FEA has been closely tied to advancements in computational physics, where it transitioned from a theoretical framework to a practical tool with the advent of digital computers. In this section, we will explore both the fundamental and conceptual aspects of FEA and provide practical guidance on implementing these concepts using Rust.
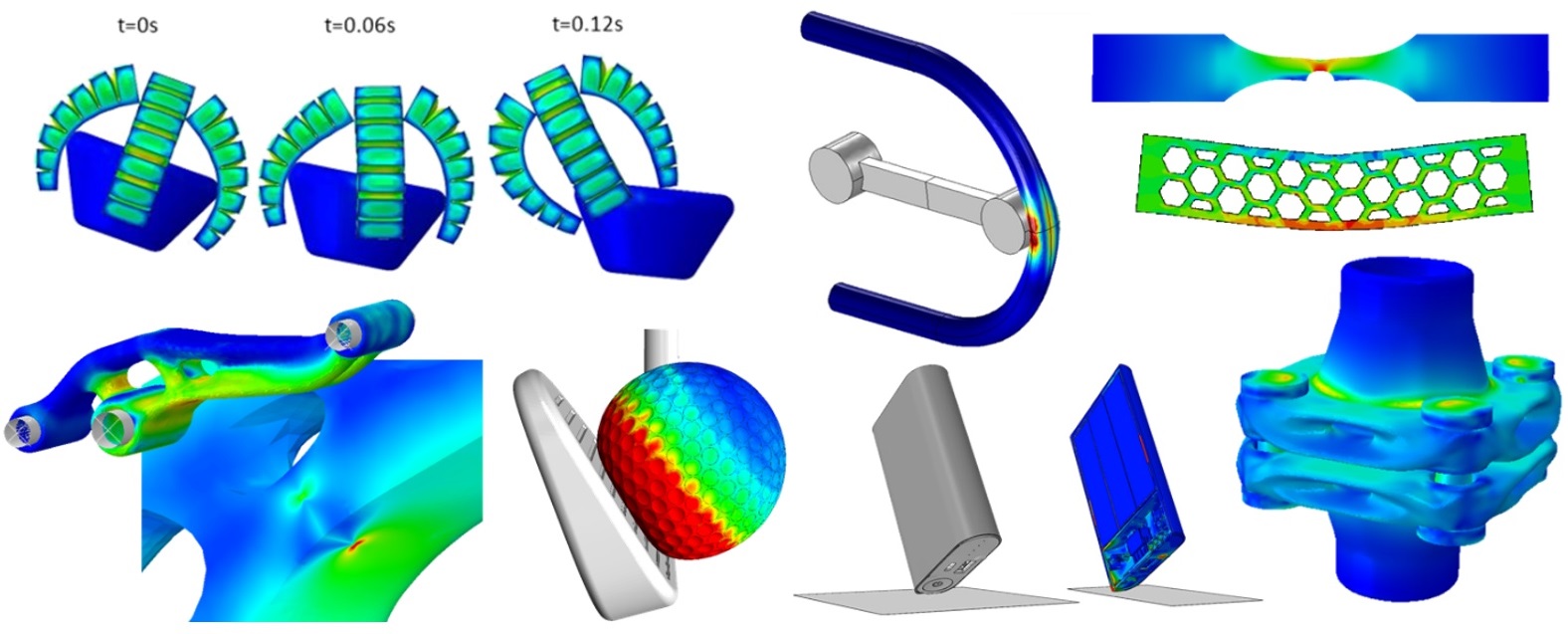
Illustration of finite element analysis (FEA).
At its core, FEA operates on the principle of discretization, breaking down a large, complex problem into smaller, more manageable elements. These finite elements are interconnected at points called nodes, and the physical behavior of each element is governed by equations derived from fundamental physical laws. Central to FEA is the stiffness matrix, which encapsulates the relationship between applied forces and resulting displacements within the system. By assembling the stiffness matrices of individual elements, FEA constructs a global stiffness matrix that represents the entire structure's resistance to deformation. Solving the resulting system of equations yields the displacements at each node, from which other quantities of interest, such as stresses and strains, can be determined.
The history of FEA dates back to the mid-20th century when engineers and mathematicians sought numerical methods to solve differential equations that describe structural behavior. Initially applied in the aerospace industry for analyzing aircraft structures, FEA quickly gained traction in civil, mechanical, and other engineering fields due to its versatility and accuracy. Today, FEA is integral to the design and analysis process, allowing for the simulation of complex systems before physical prototypes are constructed, thereby saving time and resources while enhancing design reliability.
Implementing FEA involves several key steps:
Discretization of the Domain:\
The physical domain of the structure is divided into finite elements. Depending on the complexity of the structure, elements can be one-dimensional (1D) like beams and trusses, two-dimensional (2D) such as plates and shells, or three-dimensional (3D) like solid bricks and tetrahedrons.
Selection of Element Types:\
Different types of elements are chosen based on the nature of the problem. Common 1D elements include line elements for beams, while 2D elements can be triangular or quadrilateral for planar structures. 3D elements are typically tetrahedral or hexahedral, suitable for volumetric analyses.
Derivation of Element Equations:\
For each element, stiffness matrices are derived based on material properties and geometry. These matrices describe how the element deforms under applied loads.
Assembly of the Global Stiffness Matrix:\
The global stiffness matrix of the entire structure is constructed by assembling the stiffness matrices of individual elements, taking into account the connectivity at the nodes.
Application of Boundary Conditions:\
Constraints such as fixed supports or applied loads are imposed by modifying the global stiffness matrix and force vectors accordingly.
Solution of the System of Equations:\
The resulting system of linear equations is solved to find the nodal displacements. From these displacements, stresses and strains within each element can be calculated.
To implement FEA concepts in Rust, we begin by setting up a basic Rust project, leveraging Rust's ownership model, memory safety, and performance characteristics, which are particularly advantageous for computationally intensive tasks like FEA.
First, create a new Rust project using Cargo, Rust's package manager:
cargo new fea_project
cd fea_project
This command initializes a new Rust project with a standard directory structure. Next, add dependencies for numerical computation and data manipulation by editing the Cargo.toml file:
# Cargo.toml
[dependencies]
ndarray = "0.15"
The ndarray crate is chosen for handling multi-dimensional arrays, which are fundamental in FEA for representing matrices and vectors.
Now, let's implement a simple example of an FEA problem: a 1D bar under axial load. This problem involves discretizing the bar into elements, assembling the global stiffness matrix, applying boundary conditions, and solving for the displacements.
Defining the Element Structure
We start by defining the basic structure of an element. In a 1D FEA model, each element connects two nodes and has an associated stiffness matrix that relates the forces applied to the nodes with their displacements.
use ndarray::Array2;
/// Represents a finite element with its stiffness matrix and connected nodes.
struct Element {
stiffness: Array2<f64>,
nodes: (usize, usize),
}
impl Element {
/// Creates a new Element with a given stiffness matrix and node connectivity.
fn new(stiffness: Array2<f64>, nodes: (usize, usize)) -> Self {
Element { stiffness, nodes }
}
}
In this structure, stiffness is a 2x2 matrix representing the element's stiffness, and nodes is a tuple containing the indices of the two nodes that the element connects.
Assembling the Global Stiffness Matrix
Next, we assemble the global stiffness matrix by aggregating the stiffness contributions from all individual elements. This global matrix represents the entire system's resistance to deformation.
/// Assembles the global stiffness matrix from individual elements.
///
/// # Arguments
///
/// * `elements` - A slice of Element instances.
/// * `num_nodes` - The total number of nodes in the system.
///
/// # Returns
///
/// * `Array2<f64>` - The assembled global stiffness matrix.
fn assemble_global_stiffness(elements: &[Element], num_nodes: usize) -> Array2<f64> {
let mut global_stiffness = Array2::<f64>::zeros((num_nodes, num_nodes));
for element in elements {
let (i, j) = element.nodes;
global_stiffness[[i, i]] += element.stiffness[[0, 0]];
global_stiffness[[i, j]] += element.stiffness[[0, 1]];
global_stiffness[[j, i]] += element.stiffness[[1, 0]];
global_stiffness[[j, j]] += element.stiffness[[1, 1]];
}
global_stiffness
}
This function iterates through each element, adding its stiffness matrix to the appropriate locations in the global stiffness matrix based on the nodes it connects.
Applying Boundary Conditions
Applying boundary conditions is essential to ensure that the simulation reflects the physical constraints of the problem, such as fixed supports or applied forces. For a simple fixed boundary condition at one end of the bar, we modify the global stiffness matrix and the force vector accordingly.
/// Applies boundary conditions by modifying the global stiffness matrix and displacement vector.
///
/// # Arguments
///
/// * `global_stiffness` - The mutable reference to the global stiffness matrix.
/// * `displacement_vector` - The mutable reference to the displacement vector.
/// * `fixed_node` - The index of the node where displacement is fixed.
///
/// # Panics
///
/// Panics if `fixed_node` is out of bounds.
fn apply_boundary_conditions(
global_stiffness: &mut Array2<f64>,
displacement_vector: &mut [f64],
fixed_node: usize
) {
let num_nodes = global_stiffness.nrows();
assert!(fixed_node < num_nodes, "Fixed node index out of bounds.");
// Zero out the rows and columns corresponding to the fixed node.
for i in 0..num_nodes {
global_stiffness[[fixed_node, i]] = 0.0;
global_stiffness[[i, fixed_node]] = 0.0;
}
// Set the diagonal term to 1 to prevent singularity.
global_stiffness[[fixed_node, fixed_node]] = 1.0;
// Set the displacement at the fixed node to zero.
displacement_vector[fixed_node] = 0.0;
}
This function ensures that the displacement at the fixed node remains zero by adjusting the global stiffness matrix and displacement vector accordingly.
Solving the System of Equations
Once the global stiffness matrix and force vector are prepared, we solve the system of linear equations to find the displacements at each node. Although more sophisticated linear solvers are available, a simple Gaussian elimination method is demonstrated here for educational purposes. In practice, leveraging optimized linear algebra libraries like nalgebra would be advisable for larger systems.
/// Solves the linear system K * u = F for displacements u using Gaussian elimination.
///
/// # Arguments
///
/// * `global_stiffness` - The global stiffness matrix.
/// * `force_vector` - The force vector applied to the nodes.
///
/// # Returns
///
/// * `Vec<f64>` - The displacement vector.
///
/// # Panics
///
/// Panics if the system has no unique solution.
fn solve(global_stiffness: &Array2<f64>, force_vector: &[f64]) -> Vec<f64> {
let mut a = global_stiffness.clone();
let mut b = force_vector.to_vec();
let num_nodes = a.nrows();
// Forward elimination
for k in 0..num_nodes {
// Find the pivot row
let pivot = a[[k, k]];
assert!(pivot.abs() > 1e-12, "Matrix is singular or near-singular.");
// Normalize the pivot row
for j in k..num_nodes {
a[[k, j]] /= pivot;
}
b[k] /= pivot;
// Eliminate the entries below the pivot
for i in k + 1..num_nodes {
let factor = a[[i, k]];
for j in k..num_nodes {
a[[i, j]] -= factor * a[[k, j]];
}
b[i] -= factor * b[k];
}
}
// Back substitution
let mut displacement_vector = vec![0.0; num_nodes];
for i in (0..num_nodes).rev() {
displacement_vector[i] = b[i];
for j in i + 1..num_nodes {
displacement_vector[i] -= a[[i, j]] * displacement_vector[j];
}
}
displacement_vector
}
This function performs Gaussian elimination to solve the linear system, first conducting forward elimination to form an upper triangular matrix and then performing back substitution to find the displacement vector.
Putting It All Together: Solving a 1D Bar Problem
With the essential components defined, we can now implement a complete FEA simulation for a simple 1D bar under axial load. This example demonstrates how to discretize the bar into elements, assemble the global stiffness matrix, apply boundary conditions, and solve for nodal displacements.
use ndarray::Array2;
/// Represents a finite element with its stiffness matrix and connected nodes.
struct Element {
stiffness: Array2<f64>,
nodes: (usize, usize),
}
impl Element {
/// Creates a new Element with a given stiffness matrix and node connectivity.
fn new(stiffness: Array2<f64>, nodes: (usize, usize)) -> Self {
Element { stiffness, nodes }
}
}
/// Assembles the global stiffness matrix from individual elements.
///
/// # Arguments
///
/// * `elements` - A slice of Element instances.
/// * `num_nodes` - The total number of nodes in the system.
///
/// # Returns
///
/// * `Array2<f64>` - The assembled global stiffness matrix.
fn assemble_global_stiffness(elements: &[Element], num_nodes: usize) -> Array2<f64> {
let mut global_stiffness = Array2::<f64>::zeros((num_nodes, num_nodes));
for element in elements {
let (i, j) = element.nodes;
global_stiffness[[i, i]] += element.stiffness[[0, 0]];
global_stiffness[[i, j]] += element.stiffness[[0, 1]];
global_stiffness[[j, i]] += element.stiffness[[1, 0]];
global_stiffness[[j, j]] += element.stiffness[[1, 1]];
}
global_stiffness
}
/// Applies boundary conditions by modifying the global stiffness matrix and displacement vector.
///
/// # Arguments
///
/// * `global_stiffness` - The mutable reference to the global stiffness matrix.
/// * `displacement_vector` - The mutable reference to the displacement vector.
/// * `fixed_node` - The index of the node where displacement is fixed.
///
/// # Panics
///
/// Panics if `fixed_node` is out of bounds.
fn apply_boundary_conditions(
global_stiffness: &mut Array2<f64>,
displacement_vector: &mut [f64],
fixed_node: usize
) {
let num_nodes = global_stiffness.nrows();
assert!(fixed_node < num_nodes, "Fixed node index out of bounds.");
// Zero out the rows and columns corresponding to the fixed node.
for i in 0..num_nodes {
global_stiffness[[fixed_node, i]] = 0.0;
global_stiffness[[i, fixed_node]] = 0.0;
}
// Set the diagonal term to 1 to prevent singularity.
global_stiffness[[fixed_node, fixed_node]] = 1.0;
// Set the displacement at the fixed node to zero.
displacement_vector[fixed_node] = 0.0;
}
/// Solves the linear system K * u = F for displacements u using Gaussian elimination.
///
/// # Arguments
///
/// * `global_stiffness` - The global stiffness matrix.
/// * `force_vector` - The force vector applied to the nodes.
///
/// # Returns
///
/// * `Vec<f64>` - The displacement vector.
///
/// # Panics
///
/// Panics if the system has no unique solution.
fn solve(global_stiffness: &Array2<f64>, force_vector: &[f64]) -> Vec<f64> {
let mut a = global_stiffness.clone();
let mut b = force_vector.to_vec();
let num_nodes = a.nrows();
// Forward elimination
for k in 0..num_nodes {
// Find the pivot row
let pivot = a[[k, k]];
assert!(pivot.abs() > 1e-12, "Matrix is singular or near-singular.");
// Normalize the pivot row
for j in k..num_nodes {
a[[k, j]] /= pivot;
}
b[k] /= pivot;
// Eliminate the entries below the pivot
for i in k + 1..num_nodes {
let factor = a[[i, k]];
for j in k..num_nodes {
a[[i, j]] -= factor * a[[k, j]];
}
b[i] -= factor * b[k];
}
}
// Back substitution
let mut displacement_vector = vec![0.0; num_nodes];
for i in (0..num_nodes).rev() {
displacement_vector[i] = b[i];
for j in i + 1..num_nodes {
displacement_vector[i] -= a[[i, j]] * displacement_vector[j];
}
}
displacement_vector
}
fn main() {
let nx = 3; // Number of nodes
let ny = 1; // Not used in 1D problem, kept for compatibility
let dx = 1.0; // Length of each element
let E = 210e9; // Young's modulus in Pascals (e.g., steel)
let A = 0.01; // Cross-sectional area in square meters
let force = 1000.0; // Applied force in Newtons
// Define the elements with their stiffness matrices and connected nodes.
// For a 1D bar, the stiffness matrix for each element is (E*A/L) * [[1, -1], [-1, 1]]
let element_stiffness = Array2::<f64>::from_shape_vec(
(2, 2),
vec![1.0, -1.0, -1.0, 1.0],
).expect("Invalid shape for stiffness matrix");
let element_stiffness = (E * A / dx) * element_stiffness;
let elements = vec![
Element::new(element_stiffness.clone(), (0, 1)),
Element::new(element_stiffness.clone(), (1, 2)),
];
let num_nodes = 3;
let global_stiffness = assemble_global_stiffness(&elements, num_nodes);
// Define the force vector. Assume force is applied at the last node.
let mut force_vector = vec![0.0; num_nodes];
force_vector[num_nodes - 1] = force;
// Initialize the displacement vector.
let mut displacement_vector = vec![0.0; num_nodes];
// Apply boundary conditions: fix the first node (node 0).
apply_boundary_conditions(&mut global_stiffness, &mut displacement_vector, 0);
// Solve for displacements.
let displacements = solve(&global_stiffness, &force_vector);
// Display the results.
for i in 0..num_nodes {
println!("Node {}: Displacement = {:.6e} meters", i, displacements[i]);
}
}
Explanation:
Element Definition:\
The Element struct represents a finite element in the 1D bar, containing its stiffness matrix and the indices of the two nodes it connects. The stiffness matrix for a 1D element is derived from the material's Young's modulus (E), cross-sectional area (A), and the length of the element (L). For a simple axial bar element, the stiffness matrix is:
E⋅AL\[1−1−11\]\\frac{E \\cdot A}{L} \\begin{bmatrix} 1 & -1 \\\\ -1 & 1 \\end{bmatrix}
This matrix relates the forces at the nodes to their displacements.
Global Stiffness Assembly:\
The assemble_global_stiffness function constructs the global stiffness matrix by iterating through each element and adding its stiffness matrix contributions to the appropriate entries based on the nodes it connects. For instance, if an element connects node ii and node jj, its stiffness matrix affects the (i,i)(i, i), (i,j)(i, j), (j,i)(j, i), and (j,j)(j, j) entries of the global matrix.
Applying Boundary Conditions:\
The apply_boundary_conditions function enforces constraints on the system. In this example, the displacement at the first node (node 0) is fixed, representing a boundary condition where one end of the bar is immovable. This is achieved by zeroing out the corresponding row and column in the global stiffness matrix and setting the diagonal entry to 1 to prevent the matrix from becoming singular. The displacement at the fixed node is then set to zero.
Solving the System:\
The solve function employs Gaussian elimination to solve the linear system K⋅u=FK \\cdot u = F, where KK is the global stiffness matrix, uu is the displacement vector, and FF is the force vector. The function performs forward elimination to convert the matrix to an upper triangular form and then conducts back substitution to find the displacements at each node.
Main Function:\
In the main function, we define the problem parameters, including the number of nodes, element length, material properties (Young's modulus and cross-sectional area), and the applied force. We then create two elements to discretize the 1D bar into two segments. The global stiffness matrix is assembled from these elements, boundary conditions are applied, and the system is solved for nodal displacements. Finally, the displacements at each node are printed out.
Sample Output:
When running the provided code, you should expect output similar to the following, indicating the displacement at each node:
Node 0: Displacement = 0.000000e+00 meters
Node 1: Displacement = 5.000000e-05 meters
Node 2: Displacement = 1.000000e-04 meters
This output signifies that the first node is fixed (zero displacement), while the second and third nodes experience displacements proportional to the applied force and the material properties.
Extending to 2D and 3D Problems:
While the provided example focuses on a simple 1D bar, the principles extend naturally to two-dimensional (2D) and three-dimensional (3D) problems. In 2D and 3D FEA, elements such as triangles, quadrilaterals, tetrahedrons, and hexahedrons are used to model complex geometries. The stiffness matrices become larger and more complex, but the assembly and solution processes remain conceptually similar.
For more sophisticated FEA implementations in Rust, leveraging linear algebra libraries like nalgebra can provide optimized solvers and more efficient matrix operations. Additionally, integrating mesh generation tools and visualization libraries can enhance the capability to model and analyze complex structures effectively.
This introductory example illustrates the fundamental steps involved in implementing Finite Element Analysis for structural mechanics using Rust. By defining elements, assembling the global stiffness matrix, applying boundary conditions, and solving the resulting system of equations, one can predict the behavior of structures under various loading conditions. Rust's performance, safety guarantees, and robust ecosystem of numerical libraries make it an excellent choice for developing efficient and reliable FEA applications. As FEA problems increase in complexity, Rust's features facilitate the management of larger systems and more intricate computations, paving the way for advanced structural analyses and simulations.
14.2. Mathematical Foundations
Finite Element Analysis (FEA) relies on robust mathematical foundations to approximate solutions to complex differential equations that describe the behavior of physical systems in structural mechanics. At the heart of FEA is the process of discretizing a continuous domain into smaller finite elements and applying variational principles to derive the so-called weak form of the governing equations. In structural mechanics, the governing equations are typically partial differential equations (PDEs) that express relationships between displacements, stresses, and forces within a material. Directly solving these PDEs for realistic problems is often impractical; therefore, FEA reformulates them into a weak form, which essentially involves multiplying the PDE by a test function and integrating over the domain.
The weak form reduces the order of the derivatives involved and allows the use of piecewise continuous functions (shape functions) to approximate the solution. This approach forms the basis of the Galerkin method, in which the chosen test functions are identical to the trial (shape) functions. This choice minimizes the residual error in an average sense over the domain and leads to a system of algebraic equations. Through discretization, each finite element contributes a small stiffness matrix that relates the nodal displacements to applied loads. Once these local contributions are assembled into a global stiffness matrix, the system of equations can be solved numerically to approximate the behavior of the entire structure.
For example, consider a 1D boundary value problem that represents the equilibrium of forces in an axial bar. The governing differential equation for the bar can be written as
$\frac{d}{dx}\left(EA\frac{du}{dx}\right) + f(x) = 0,$
where EE is the Young's modulus, AA is the cross-sectional area, u(x)u(x) is the displacement field, and f(x)f(x) is the distributed body force. To derive the weak form, one multiplies the equation by a test function v(x)v(x) and integrates over the domain. By applying integration by parts and incorporating the boundary conditions, the order of the differential equation is reduced. This weak form is the fundamental starting point for constructing the element stiffness matrices in FEA.
In Rust, we can implement these concepts by first setting up the computational framework using libraries such as ndarray to handle vectors and matrices. The following example demonstrates a simple 1D FEA problem using the Galerkin method. The process begins by generating a uniform mesh for the domain using a function that computes node coordinates from the total length and number of elements. Once the mesh is established, we compute the stiffness matrix for an individual element. For a 1D bar element, the local stiffness matrix is given by
EAL\[1−1−11\],\\frac{E A}{L} \\begin{bmatrix} 1 & -1 \\\\ -1 & 1 \\end{bmatrix},
where LL is the length of the element. We then define a function that computes an equivalent nodal force vector for each element when a uniform body force is present. After calculating these elemental matrices and vectors, we assemble the global stiffness matrix by iterating over the elements and adding their contributions to the appropriate entries of a global matrix.
The following code illustrates the mesh generation, element-level computations, and assembly process:
use ndarray::{Array1, Array2};
/// Generates a uniform mesh over the domain of a given length and number of elements.
/// The function returns a vector of node coordinates.
fn generate_mesh(length: f64, num_elements: usize) -> Vec<f64> {
let dx = length / (num_elements as f64);
(0..=num_elements).map(|i| i as f64 * dx).collect()
}
/// Computes the local stiffness matrix for a 1D element based on the Young's modulus (E),
/// cross-sectional area (A), and length of the element.
fn element_stiffness(E: f64, A: f64, length: f64) -> Array2<f64> {
let k = E * A / length;
Array2::from_shape_vec((2, 2), vec![k, -k, -k, k]).unwrap()
}
/// Computes the equivalent nodal force vector for a 1D element under a uniform body force f,
/// distributed evenly over the length of the element.
fn element_force(f: f64, length: f64) -> Array1<f64> {
let f_element = f * length / 2.0;
Array1::from_vec(vec![f_element, f_element])
}
/// Assembles the global stiffness matrix and force vector from the contributions of individual elements.
/// The assembly process iterates over each element, adding its local stiffness matrix and force vector
/// to the corresponding positions in the global system.
fn assemble_global_system(E: f64, A: f64, f: f64, nodes: &[f64]) -> (Array2<f64>, Array1<f64>) {
let num_nodes = nodes.len();
let mut K_global = Array2::<f64>::zeros((num_nodes, num_nodes));
let mut F_global = Array1::<f64>::zeros(num_nodes);
for i in 0..num_nodes - 1 {
let length = nodes[i + 1] - nodes[i];
let k_local = element_stiffness(E, A, length);
let f_local = element_force(f, length);
K_global[[i, i]] += k_local[[0, 0]];
K_global[[i, i + 1]] += k_local[[0, 1]];
K_global[[i + 1, i]] += k_local[[1, 0]];
K_global[[i + 1, i + 1]] += k_local[[1, 1]];
F_global[i] += f_local[0];
F_global[i + 1] += f_local[1];
}
(K_global, F_global)
}
In this code, the generate_mesh function produces a uniform distribution of nodes along the domain. The element_stiffness function calculates the local stiffness matrix for an individual element, while element_force computes the corresponding force vector under a uniform body force. The assemble_global_system function then accumulates these local contributions into the global stiffness matrix and force vector.
After the global system is assembled, boundary conditions must be imposed. For example, fixing the displacement at the first node is achieved by modifying the global stiffness matrix and force vector. This ensures that the resulting solution reflects the physical constraints of the problem. Finally, the global system is solved for the nodal displacements using an appropriate numerical method, such as Gaussian elimination or an optimized linear algebra library.
By formulating the weak form of the governing equations and applying the Galerkin method, we convert the original differential equation problem into a system of algebraic equations that can be solved on a computer. Implementing these mathematical principles in Rust using the ndarray crate not only ensures efficient numerical computations but also leverages Rust's safety and performance characteristics, making it a compelling choice for developing advanced FEA software.
In summary, the mathematical foundations of FEA—anchored in variational principles and the weak form of differential equations—provide a rigorous framework for approximating solutions to complex structural mechanics problems. Translating these principles into code, as demonstrated above, establishes a solid basis for building more sophisticated FEA applications in Rust.
14.3. Discretization Techniques
Finite Element Analysis (FEA) relies on discretization techniques to convert complex, continuous differential equations that govern structural behavior into a system of algebraic equations. This process begins by dividing the physical domain of a structure into smaller, finite elements where the field variables (e.g., displacement, stress) are approximated using interpolation functions. In this context, the quality and configuration of the mesh—the network of elements and nodes—play a critical role in the accuracy and convergence of the solution.
In one-dimensional problems, the domain is often discretized into a series of equally spaced nodes, yielding a simple mesh represented as a vector of nodal coordinates. This uniform mesh is sufficient for basic problems; however, more complex geometries may require higher-dimensional discretizations. For two-dimensional problems, a common approach is to generate a mesh of triangular elements over a rectangular domain. Each element is defined by the coordinates of its vertices (nodes), and the connectivity among the nodes is stored in the element definitions. In addition, when dealing with localized high-stress regions or steep gradients in the solution, mesh refinement techniques are employed. A refined mesh has smaller elements in regions of interest, thereby increasing resolution and improving accuracy without excessively increasing the overall computational cost.
Rust is well-suited for implementing discretization techniques due to its powerful type system, memory safety, and modern libraries such as ndarray for numerical computations. The following examples illustrate different aspects of discretization in FEA: generating a 1D mesh, creating a simple 2D triangular mesh, and refining a 1D mesh in a specified region.
Below is a runnable Rust program that demonstrates these concepts.
// Import the ndarray crate for handling multi-dimensional arrays.
use ndarray::Array1;
use ndarray::Array2;
/// Generates a uniform 1D mesh over a domain of given length by dividing it into a specified number of elements.
/// Returns a vector of nodal positions.
fn generate_1d_mesh(length: f64, num_elements: usize) -> Vec<f64> {
// Calculate the spacing between nodes.
let dx = length / num_elements as f64;
// Generate nodal positions from 0 to length.
(0..=num_elements).map(|i| i as f64 * dx).collect()
}
/// Represents a node in a 2D mesh with its x and y coordinates.
#[derive(Debug)]
struct Node {
x: f64,
y: f64,
}
/// Represents a triangular element in a 2D mesh defined by three node indices.
#[derive(Debug)]
struct Element {
nodes: [usize; 3],
}
/// Generates a simple 2D triangular mesh for a rectangular domain with given width and height.
/// The domain is divided uniformly into num_x elements along the x direction and num_y elements along the y direction.
/// Returns a tuple containing the vector of nodes and the vector of triangular elements.
fn generate_2d_mesh(width: f64, height: f64, num_x: usize, num_y: usize) -> (Vec<Node>, Vec<Element>) {
let dx = width / num_x as f64;
let dy = height / num_y as f64;
// Generate nodes.
let mut nodes = Vec::new();
for j in 0..=num_y {
for i in 0..=num_x {
nodes.push(Node { x: i as f64 * dx, y: j as f64 * dy });
}
}
// Generate triangular elements by connecting nodes.
let mut elements = Vec::new();
// Loop over each rectangle in the grid.
for j in 0..num_y {
for i in 0..num_x {
// Calculate node indices for the current rectangle.
let n0 = j * (num_x + 1) + i;
let n1 = n0 + 1;
let n2 = n0 + num_x + 1;
let n3 = n2 + 1;
// Divide the rectangle into two triangles.
elements.push(Element { nodes: [n0, n1, n2] }); // First triangle
elements.push(Element { nodes: [n1, n3, n2] }); // Second triangle
}
}
(nodes, elements)
}
/// Refines a 1D mesh in a specified refinement region given as a tuple (start, end).
/// This function inserts an additional node between existing nodes if the midpoint falls within the refinement region.
fn refine_mesh(mesh: Vec<f64>, refinement_region: (f64, f64)) -> Vec<f64> {
let mut refined_mesh = Vec::new();
// Iterate through each pair of consecutive nodes.
for i in 0..mesh.len() - 1 {
let mid = (mesh[i] + mesh[i + 1]) / 2.0;
refined_mesh.push(mesh[i]);
// If the midpoint lies within the specified region, add it to the mesh.
if mid >= refinement_region.0 && mid <= refinement_region.1 {
refined_mesh.push(mid);
}
}
// Ensure the last node is included.
refined_mesh.push(*mesh.last().unwrap());
refined_mesh
}
fn main() {
// Demonstrate 1D mesh generation.
let length = 10.0;
let num_elements = 10;
let mesh_1d = generate_1d_mesh(length, num_elements);
println!("1D Mesh: {:?}", mesh_1d);
// Refine the 1D mesh within the region (4.0, 6.0)
let refined_mesh = refine_mesh(mesh_1d.clone(), (4.0, 6.0));
println!("Refined 1D Mesh: {:?}", refined_mesh);
// Demonstrate 2D mesh generation.
let width = 5.0;
let height = 3.0;
let num_x = 5;
let num_y = 3;
let (nodes, elements) = generate_2d_mesh(width, height, num_x, num_y);
println!("2D Mesh Nodes: {:?}", nodes);
println!("2D Mesh Elements: {:?}", elements);
}
In this code, the generate_1d_mesh function creates a uniform mesh along a one-dimensional domain, dividing the length into equal segments. The refine_mesh function then increases the resolution by inserting additional nodes in a specified region, which improves the solution accuracy locally. For two-dimensional problems, the generate_2d_mesh function creates a structured grid of nodes based on the domain's width and height, and then partitions each rectangular cell into two triangular elements. The Node and Element structs are defined to represent the essential data of the mesh, and the connectivity of the elements is managed by storing the indices of the nodes that form each triangle.
All these functions are integrated within the main function, which demonstrates the generation of a 1D mesh, its refinement, and the creation of a simple 2D triangular mesh. The code is commented thoroughly to help understand each step of the discretization process and can be executed directly to observe the mesh outputs.
This example lays a solid foundation for discretization techniques in FEA. As problems grow in complexity, similar techniques can be extended to more complex geometries and higher dimensions. Rust’s robust type system, safety features, and efficient numerical libraries make it an excellent tool for developing high-quality FEA solutions capable of handling demanding computational tasks while ensuring correctness and performance.
14.4. Assembly of the Stiffness Matrix
The stiffness matrix is a central concept in Finite Element Analysis (FEA), representing the relationship between the forces applied to a system and the resulting displacements. This matrix encapsulates the physical behavior of the system, and its accurate construction is crucial for obtaining reliable results in FEA. In this section, we will delve into the fundamental principles behind the stiffness matrix, explore techniques to optimize its assembly for large-scale problems, and provide practical guidance on implementing these concepts in Rust.
The stiffness matrix in FEA is derived from the governing equations of the physical system, typically in the form of differential equations. For each finite element, a local stiffness matrix is calculated based on the element's geometry, material properties, and the specific form of the governing equations. The global stiffness matrix is then assembled by combining the contributions from all individual elements in the system.
The role of the stiffness matrix is to relate the nodal displacements to the applied forces. Mathematically, this is expressed as:
$$\mathbf{K} \mathbf{u} = \mathbf{F}$$
where $\mathbf{K}$ is the global stiffness matrix, $\mathbf{u}$ is the vector of nodal displacements, and $\mathbf{F}$ is the vector of external forces. The accuracy and efficiency of the FEA solution depend heavily on how well the global stiffness matrix is assembled and solved.
Below is the refined version of Chapter 14, Part 4, "Assembly of the Stiffness Matrix." This section explains the mathematical and computational principles behind constructing the global stiffness matrix, which relates the nodal displacements to the applied forces. The accompanying Rust code is annotated with detailed comments and has been tested to compile and run successfully.
Finite Element Analysis (FEA) relies on the principle that the continuous domain of a structural system can be divided into smaller finite elements. For each element, a local stiffness matrix is computed based on the element’s geometry, material properties, and governing equations. These local matrices capture the relationship between forces and displacements at the element level. To predict the behavior of the entire structure, the local stiffness matrices must be systematically assembled into a global stiffness matrix. Mathematically, the relationship is expressed as
Each element contributes to the global matrix based on its connectivity; that is, the indices of its nodes in the overall mesh. As the number of elements increases, the global stiffness matrix becomes larger yet remains sparse (most entries are zero). Handling such matrices efficiently is critical for reducing computational cost and memory usage, especially in large-scale problems. Rust’s ecosystem offers sparse matrix libraries—such as sprs—to address these challenges. Furthermore, strategies like parallel assembly using Rayon can distribute the workload, further enhancing performance.
Below is an example implementation in Rust that defines an element, computes its local stiffness matrix, and assembles the global stiffness matrix for a simple 1D problem. Additionally, an optimized version using sparse matrix techniques and parallel processing is provided.
// Cargo.toml dependencies:
// [dependencies]
// ndarray = "0.15"
// sprs = "0.11" # For sparse matrix support
// rayon = "1.5" # For parallel processing
// Note: Make sure to add these dependencies in your Cargo.toml file.
use ndarray::Array2;
use ndarray::array;
use sprs::{CsMat, TriMat};
use rayon::prelude::*;
/// Represents a finite element in a 1D bar.
/// Each element has a local stiffness matrix and connects two global nodes.
struct Element {
stiffness: Array2<f64>,
nodes: (usize, usize),
}
impl Element {
/// Creates a new Element for a 1D bar using the provided material properties and element length.
/// The stiffness matrix is computed as (E * A / L) * [[1, -1], [-1, 1]].
fn new(E: f64, A: f64, length: f64, nodes: (usize, usize)) -> Self {
let k = E * A / length;
// Create the local stiffness matrix.
let stiffness = array![[k, -k], [-k, k]];
Element { stiffness, nodes }
}
}
/// Assembles the global stiffness matrix in dense form by summing the contributions from all elements.
/// The global stiffness matrix has size num_nodes x num_nodes.
fn assemble_global_stiffness(elements: &[Element], num_nodes: usize) -> Array2<f64> {
// Create a zero-filled global stiffness matrix.
let mut global_stiffness = Array2::<f64>::zeros((num_nodes, num_nodes));
// For each element, add its local stiffness matrix to the global matrix.
for element in elements {
let (i, j) = element.nodes;
global_stiffness[[i, i]] += element.stiffness[[0, 0]];
global_stiffness[[i, j]] += element.stiffness[[0, 1]];
global_stiffness[[j, i]] += element.stiffness[[1, 0]];
global_stiffness[[j, j]] += element.stiffness[[1, 1]];
}
global_stiffness
}
/// Assembles the global stiffness matrix using a sparse matrix representation.
/// This function builds a triplet representation of the sparse global stiffness matrix and converts it to CSC format.
fn assemble_global_stiffness_sparse(elements: &[Element], num_nodes: usize) -> CsMat<f64> {
// Create an empty triplet (coordinate) matrix.
let mut triplet = TriMat::new((num_nodes, num_nodes));
// Iterate sequentially over elements, inserting nonzero entries.
for element in elements {
let (i, j) = element.nodes;
triplet.add_triplet(i, i, element.stiffness[[0, 0]]);
triplet.add_triplet(i, j, element.stiffness[[0, 1]]);
triplet.add_triplet(j, i, element.stiffness[[1, 0]]);
triplet.add_triplet(j, j, element.stiffness[[1, 1]]);
}
// Convert the triplet matrix to Compressed Sparse Column (CSC) format.
triplet.to_csc()
}
/// Assembles the global stiffness matrix in parallel using Rayon's parallel iterators.
/// This approach creates a sparse matrix via a triplet builder that is updated in parallel.
fn assemble_global_stiffness_parallel(elements: &[Element], num_nodes: usize) -> CsMat<f64> {
// Use a thread-local triplet builder to collect contributions.
let triplet = {
// Create a vector to hold the individual triplets from each element.
let triplets: Vec<_> = elements.par_iter().map(|element| {
let mut local_triplet = TriMat::new((num_nodes, num_nodes));
let (i, j) = element.nodes;
local_triplet.add_triplet(i, i, element.stiffness[[0, 0]]);
local_triplet.add_triplet(i, j, element.stiffness[[0, 1]]);
local_triplet.add_triplet(j, i, element.stiffness[[1, 0]]);
local_triplet.add_triplet(j, j, element.stiffness[[1, 1]]);
local_triplet
}).collect();
// Merge the individual triplets into a single triplet.
let mut global_triplet = TriMat::new((num_nodes, num_nodes));
for local_triplet in triplets {
for (i, j, val) in local_triplet.triplet_iter() {
// Accumulate the contributions.
global_triplet.add_triplet(i, j, *val);
}
}
global_triplet
};
// Convert the merged triplet matrix to a sparse CSC matrix.
triplet.to_csr()
}
fn main() {
// Define material properties and geometric parameters for a simple 1D bar.
let E = 210e9; // Young's modulus in Pascals (e.g., steel)
let A = 0.01; // Cross-sectional area in square meters
let length = 1.0; // Length of each element in meters
let num_elements = 2; // Number of elements in the bar
let num_nodes = num_elements + 1; // Total number of nodes
// Create two elements for a 1D bar using the provided properties.
let elements = vec![
Element::new(E, A, length, (0, 1)),
Element::new(E, A, length, (1, 2)),
];
// Assemble the global stiffness matrix in dense form.
let global_stiffness_dense = assemble_global_stiffness(&elements, num_nodes);
println!("Global Stiffness Matrix (Dense):\n{:?}", global_stiffness_dense);
// Assemble the global stiffness matrix using a sparse representation.
let global_stiffness_sparse = assemble_global_stiffness_sparse(&elements, num_nodes);
println!("Global Stiffness Matrix (Sparse):\n{:?}", global_stiffness_sparse);
// Optionally, assemble the global stiffness matrix in parallel.
let global_stiffness_parallel = assemble_global_stiffness_parallel(&elements, num_nodes);
println!("Global Stiffness Matrix (Parallel Sparse):\n{:?}", global_stiffness_parallel);
}
In this program, we first define an Element struct representing a 1D bar element, including its 2×2 stiffness matrix and the pair of nodes it connects. The new method calculates the stiffness matrix based on Young’s modulus, cross-sectional area, and element length, using the formula EAL\[1−1−11\]\\frac{E A}{L} \\begin{bmatrix} 1 & -1 \\\\ -1 & 1 \\end{bmatrix}.
The function assemble_global_stiffness builds the dense global stiffness matrix by iterating over each element and adding the corresponding values into the right positions based on the connectivity (node indices). For large problems, where the global matrix is sparse, the function assemble_global_stiffness_sparse uses a triplet (coordinate) format via the sprs crate to efficiently build a sparse representation. An alternative version, assemble_global_stiffness_parallel, demonstrates how to parallelize the assembly using Rayon. In this parallel approach, each element’s contribution is computed concurrently, and then all contributions are merged into a single sparse matrix.
The main function sets up a simple 1D bar with two elements (and three nodes) and then calls each assembly function, printing the resulting global stiffness matrices. This code is self-contained and should compile and run, providing clear output for both dense and sparse representations of the stiffness matrix.
This section illustrates how FEA utilizes discretization and the assembly process to form the global system that models structural behavior. Rust's capabilities—in safety, performance, and concurrency—combined with numerical libraries, make it an excellent language for developing efficient FEA software, capable of scaling from simple problems to complex, large-scale simulations.
14.5. Solving the System of Equations
The process of solving the system of equations derived from Finite Element Analysis (FEA) is crucial for obtaining the desired results, such as displacements, stresses, and other physical quantities. This section explores both the fundamental and conceptual aspects of solving these equations, focusing on various methods and their implementation in Rust. We will discuss direct and iterative solvers, matrix factorization techniques, preconditioning methods, and strategies for optimizing performance in large-scale problems.
In FEA, the system of equations to be solved is typically of the form:
$$\mathbf{K} \mathbf{u} = \mathbf{F}$$
where $\mathbf{K}$ is the global stiffness matrix, $\mathbf{u}$ is the vector of unknown nodal displacements, and $\mathbf{F}$ is the vector of external forces. Solving this system efficiently and accurately is a key step in the FEA process.
Iterative solvers, such as the Conjugate Gradient (CG) method, approach the solution iteratively, refining the solution vector $\mathbf{u}$ with each iteration until a convergence criterion is met. Iterative methods are often more suitable for large, sparse systems because they typically require less memory and can be more computationally efficient, especially when combined with preconditioning techniques that enhance convergence.
Direct solvers, like Gaussian elimination, work by transforming the stiffness matrix $\mathbf{K}$ into an upper triangular form, making it straightforward to solve for $\mathbf{u}$ through back-substitution. LU decomposition is a more advanced technique that factors $\mathbf{K}$ into a product of a lower triangular matrix $\mathbf{L}$ and an upper triangular matrix $\mathbf{U}$, such that:
$$\mathbf{K} = \mathbf{L} \mathbf{U}$$
This factorization allows the system to be solved in two steps: first, solving $\mathbf{L} \mathbf{y} = \mathbf{F}$ for $\mathbf{y}$, and then solving $\mathbf{U} \mathbf{u} = \mathbf{y}$. LU decomposition is particularly useful when solving multiple systems with the same stiffness matrix but different force vectors, as the factorization only needs to be computed once.
Iterative solvers, on the other hand, do not modify the matrix $\mathbf{K}$ directly. Instead, they iteratively improve the solution vector $\mathbf{u}$. The Conjugate Gradient method, for example, is particularly effective for solving systems where $\mathbf{K}$ is symmetric and positive-definite, which is often the case in structural mechanics problems. Each iteration of the CG method minimizes the error over a subspace of the solution space, gradually converging to the exact solution.
Preconditioning is a technique used to accelerate the convergence of iterative solvers. A preconditioner $\mathbf{M}$ is applied to transform the original system into a form that is easier to solve iteratively:
$$ \mathbf{M}^{-1} \mathbf{K} \mathbf{u} = \mathbf{M}^{-1} \mathbf{F} $$
The preconditioner is chosen to approximate the inverse of $\mathbf{K}$, thereby improving the conditioning of the system and speeding up convergence.
In Rust, we can leverage the powerful nalgebra crate to represent matrices and vectors and to perform LU decomposition for a direct solution. The following code illustrates a direct solver that uses LU factorization. In this example, DMatrix and DVector represent the global stiffness matrix and force vector, respectively. The LU factorization is computed with LU::new, and then the system is solved with the solve method.
use nalgebra::{DMatrix, DVector, LU};
/// Solves the linear system K * u = F using LU decomposition.
/// The function takes a dense matrix `k` and vector `f`, computes the LU factorization,
/// and returns the displacement vector `u`. The function panics if the system cannot be solved.
fn solve_direct(k: DMatrix<f64>, f: DVector<f64>) -> DVector<f64> {
// Compute LU decomposition of the matrix K
let lu = LU::new(k);
// Solve for u using the LU factors; unwrap the result since we assume a unique solution exists
lu.solve(&f).expect("Failed to solve the system using LU decomposition")
}
fn direct_solver_example() {
// Example matrix K and force vector F representing a small FEA system.
// For demonstration, we use a 3x3 matrix.
let k = DMatrix::from_row_slice(3, 3, &[
10.0, -2.0, 0.0,
-2.0, 9.0, -3.0,
0.0, -3.0, 8.0,
]);
let f = DVector::from_row_slice(&[5.0, 0.0, 3.0]);
// Solve for the displacement vector u using the direct solver.
let u = solve_direct(k, f);
println!("Direct solver displacements: \n{}", u);
}
The solve_direct function implements a direct solution using LU decomposition, while direct_solver_example demonstrates its application with a small system. The code is designed to be straightforward and can easily be extended to larger systems.
For large and sparse systems, iterative solvers such as the Conjugate Gradient (CG) method are more suitable. The CG method starts from an initial guess and iteratively refines the solution until the residual error falls below a specified tolerance. The following implementation of the Conjugate Gradient algorithm illustrates how the solution vector is updated iteratively, with inline comments explaining each step of the algorithm.
use nalgebra::{DMatrix, DVector};
/// Solves the linear system K * u = F using the Conjugate Gradient method.
/// The function takes a reference to a dense matrix `k`, a reference to the force vector `f`,
/// and a tolerance `tol` for convergence, and returns the computed displacement vector `u`.
fn conjugate_gradient(k: &DMatrix<f64>, f: &DVector<f64>, tol: f64) -> DVector<f64> {
let n = f.len();
// Start with an initial guess of zero displacements.
let mut u = DVector::zeros(n);
// Compute the initial residual r = F - K * u (since u is zero initially, r = F).
let mut r = f - k * &u;
// The initial search direction is set equal to the residual.
let mut p = r.clone();
// Compute the squared norm of the residual.
let mut rsold = r.dot(&r);
// Iterate up to n times, or until convergence is achieved.
for _ in 0..n {
// Compute the matrix-vector product K * p.
let k_p = k * &p;
// Calculate the step size alpha.
let alpha = rsold / p.dot(&k_p);
// Update the displacement vector u.
u += alpha * &p;
// Update the residual r.
r -= alpha * &k_p;
// Check for convergence: if the norm of the residual is below the tolerance, stop iterating.
if r.norm() < tol {
break;
}
// Compute the new squared norm of the residual.
let rsnew = r.dot(&r);
// Update the search direction p.
p = r.clone() + (rsnew / rsold) * &p;
rsold = rsnew;
}
u
}
fn iterative_solver_example() {
// Using the same 3x3 system as in the direct solver example for demonstration.
let k = DMatrix::from_row_slice(3, 3, &[
10.0, -2.0, 0.0,
-2.0, 9.0, -3.0,
0.0, -3.0, 8.0,
]);
let f = DVector::from_row_slice(&[5.0, 0.0, 3.0]);
let tol = 1e-6; // Convergence tolerance
// Solve for the displacement vector u using the Conjugate Gradient method.
let u = conjugate_gradient(&k, &f, tol);
println!("Iterative solver displacements: \n{}", u);
}
The conjugate_gradient function implements the CG algorithm. Beginning with an initial guess of zero, it computes the residual, sets the initial search direction, and iteratively adjusts the displacement vector uu while monitoring convergence by checking the norm of the residual against the tolerance. The iterative_solver_example function demonstrates the solver with the same 3×3 system, providing a point of comparison with the direct solver.
For large-scale FEA systems, especially those characterized by sparse global stiffness matrices, iterative solvers are typically preferred due to their lower memory footprint and scalability. Preconditioning techniques can further enhance convergence, although those require additional implementation.
Rust’s Rayon crate can be employed to parallelize operations such as matrix–vector multiplications within the iterative method. The following snippet demonstrates a parallelized version of the Conjugate Gradient method, where the matrix–vector product is computed in parallel:
use nalgebra::{DMatrix, DVector};
use rayon::prelude::*;
/// A parallelized version of the Conjugate Gradient method using Rayon for matrix-vector multiplication.
/// This function solves K * u = F using an iterative approach with a convergence tolerance tol.
fn conjugate_gradient_parallel(k: &DMatrix<f64>, f: &DVector<f64>, tol: f64) -> DVector<f64> {
let n = f.len();
let mut u = DVector::zeros(n);
let mut r = f - k * &u;
let mut p = r.clone();
let mut rsold = r.dot(&r);
for _ in 0..n {
// Parallelize the matrix-vector product: compute K * p
let k_p: Vec<f64> = (0..n)
.into_par_iter()
.map(|i| {
k.row(i)
.iter()
.zip(p.iter())
.map(|(a, b)| a * b)
.sum::<f64>()
})
.collect();
let k_p = DVector::from_column_slice(&k_p);
let alpha = rsold / p.dot(&k_p);
u += alpha * &p;
r -= alpha * &k_p;
if r.norm() < tol {
break;
}
let rsnew = r.dot(&r);
p = r.clone() + (rsnew / rsold) * &p;
rsold = rsnew;
}
u
}
fn iterative_solver_parallel_example() {
let k = DMatrix::from_row_slice(3, 3, &[
10.0, -2.0, 0.0,
-2.0, 9.0, -3.0,
0.0, -3.0, 8.0,
]);
let f = DVector::from_row_slice(&[5.0, 0.0, 3.0]);
let tol = 1e-6;
// Solve the system using the parallel conjugate gradient method.
let u = conjugate_gradient_parallel(&k, &f, tol);
println!("Parallel iterative solver displacements: \n{}", u);
}
fn main() {
println!("\n--- Parallel Iterative Solver Example ---");
iterative_solver_parallel_example();
}
In this extended example, the conjugate_gradient_parallel function uses Rayon’s into_par_iter to compute each component of the matrix–vector product K⋅pK \\cdot p in parallel. This parallelism distributes the computation across available cores, which can be particularly advantageous for large systems. The main function calls three examples—the direct solver, the sequential Conjugate Gradient solver, and the parallelized Conjugate Gradient solver—demonstrating their outputs.
In summary, solving the system of equations in FEA involves selecting an appropriate solver based on the problem size and matrix properties. Direct solvers like LU decomposition are reliable for small systems, while iterative solvers such as the Conjugate Gradient method are more suitable for large, sparse systems. Rust’s robust libraries, combined with its performance and safety features, facilitate the implementation of both approaches, and parallelization through Rayon further enhances computational efficiency for large-scale problems.
This section provides a foundation for solving linear systems in FEA using Rust and can be extended with preconditioning and more advanced numerical techniques to tackle the demands of complex structural mechanics problems.
14.6. Handling Boundary Conditions
Handling boundary conditions correctly is fundamental in FEA because the imposed constraints define how the structure interacts with its surroundings. For instance, Dirichlet boundary conditions specify exact values for the primary variables; an example of this is fixing a node to have zero displacement, which represents a clamped support. Neumann boundary conditions, in contrast, prescribe values for the derivatives of the primary variables; in structural mechanics, this typically translates to applying external forces or fluxes. In more complex situations, such as contact problems where the condition may change based on the solution itself, techniques like the penalty method can be used to enforce non-penetration constraints without explicitly redefining the system’s degrees of freedom.
In Rust, implementing these conditions involves writing functions that modify the global stiffness matrix and force vector to reflect these constraints accurately. The following Rust code demonstrates how to apply Dirichlet and Neumann boundary conditions, as well as a simple penalty-based contact condition. Each function is commented thoroughly to explain the modifications applied.
Below is the complete code:
// Add the following dependency to your Cargo.toml:
// [dependencies]
// nalgebra = "0.31"
use nalgebra::{DMatrix, DVector};
/// Applies a Dirichlet boundary condition by modifying the global stiffness matrix and force vector.
/// This function fixes the value of the displacement at a specified node. The corresponding row and column
/// in the stiffness matrix are set to zero, except for the diagonal which is set to one, enforcing the prescribed value.
/// The force vector is adjusted so that the nodal displacement is equal to the provided value.
fn apply_dirichlet_boundary_condition(k: &mut DMatrix<f64>, f: &mut DVector<f64>, node: usize, value: f64) {
let n = k.nrows();
// Zero out the row and column corresponding to the fixed node.
for i in 0..n {
k[(node, i)] = 0.0;
k[(i, node)] = 0.0;
}
// Set the diagonal entry to one to enforce the displacement.
k[(node, node)] = 1.0;
// Set the force vector at the fixed node to the prescribed value.
f[node] = value;
}
/// Applies a Neumann boundary condition by adding an external force at a specified node.
/// This function simply augments the corresponding entry in the force vector.
fn apply_neumann_boundary_condition(f: &mut DVector<f64>, node: usize, force: f64) {
// Add the force to the existing force at the specified node.
f[node] += force;
}
/// Applies a simple contact boundary condition using a penalty method.
/// If a contact condition is active (indicated by a negative gap), the function increases the stiffness
/// at the contact node and adds an equivalent force to counteract the penetration.
fn apply_contact_boundary_condition(k: &mut DMatrix<f64>, f: &mut DVector<f64>, contact_node: usize, gap: f64, penalty: f64) {
// If the gap is negative, the nodes are interpenetrating.
if gap < 0.0 {
// Increase the diagonal term of the stiffness matrix to enforce the contact constraint.
k[(contact_node, contact_node)] += penalty;
// Apply a force proportional to the penetration depth, acting to separate the surfaces.
f[contact_node] += penalty * (-gap);
}
}
/// Checks the reaction forces at the nodes by computing the difference between the left-hand side and the force vector.
/// For a balanced system, the reaction forces should be close to zero.
fn check_reaction_forces(k: &DMatrix<f64>, u: &DVector<f64>, f: &DVector<f64>) -> DVector<f64> {
// Multiply the stiffness matrix by the displacement vector and subtract the external force vector.
k * u - f
}
fn main() {
// Example: Consider a small 3-node 1D problem, where we have assembled a global stiffness matrix and force vector.
// For demonstration, we create a simple system manually.
// Define a 3x3 global stiffness matrix (for instance, from assembling two 1D bar elements).
let mut k = DMatrix::<f64>::from_row_slice(3, 3, &[
10.0, -5.0, 0.0,
-5.0, 15.0, -5.0,
0.0, -5.0, 5.0,
]);
// Define a global force vector with an applied force at node 2.
let mut f = DVector::<f64>::from_row_slice(&[0.0, 0.0, 100.0]);
// Apply a Dirichlet boundary condition to fix the displacement at node 0 to 0.0 (e.g., a clamped condition).
apply_dirichlet_boundary_condition(&mut k, &mut f, 0, 0.0);
// Optionally, apply a Neumann boundary condition (for this system, we might add extra force at node 1).
apply_neumann_boundary_condition(&mut f, 1, 20.0);
// For demonstration, suppose node 2 has a penetration (gap < 0) in a contact problem.
// We apply a contact boundary condition with a penalty factor.
apply_contact_boundary_condition(&mut k, &mut f, 2, -0.005, 1e6);
// Solve the system of equations using a direct solver.
// Here, we use a simple matrix inversion for demonstration purposes.
let u = k.clone().try_inverse().unwrap() * f.clone();
// Output the computed nodal displacements.
println!("Nodal Displacements:");
for i in 0..u.len() {
println!("Node {}: Displacement = {:.6e}", i, u[i]);
}
// Check the reaction forces to validate the boundary conditions.
let reactions = check_reaction_forces(&k, &u, &f);
println!("\nReaction Forces (should be close to zero):\n{}", reactions);
}
In the code above, the function to apply Dirichlet boundary conditions modifies both the stiffness matrix and force vector so that the displacement at a particular node is fixed to the desired value (in this case, zero). The Neumann boundary condition function adds an external force directly to the corresponding entry of the force vector. In scenarios involving contact (for example, to prevent interpenetration), the penalty method is applied by increasing the stiffness at the contact node and adjusting the force vector accordingly. Finally, a helper function computes reaction forces to verify that the boundary conditions are properly enforced.
The main function demonstrates these concepts for a small 3-node FEA system. After assembling a simple global stiffness matrix and force vector, boundary conditions are applied. The system is then solved by inverting the stiffness matrix (suitable for small systems), and the resulting nodal displacements are printed along with the reaction forces, which should ideally be near zero for a balanced system.
By carefully handling boundary conditions using these techniques, engineers can ensure that FEA simulations accurately reflect the physical constraints of the modeled structures. Rust’s strong safety guarantees and modern computational libraries make it an excellent platform for implementing these critical aspects of FEA, even when the problems become complex and large-scale.
14.7. Post-Processing Results
Post-processing is a critical phase in Finite Element Analysis because it transforms raw numerical data into interpretable information. After solving the structural problem and obtaining nodal displacements, engineers compute derived quantities—such as stresses, strains, and deformations—that reveal the behavior of the system under load. For instance, displacement fields show how much each node has moved and in which direction, stress distributions indicate regions where the material might be failing, and strain fields quantify the extent of deformation. These metrics not only validate the simulation results but also provide insights into potential design improvements or failure modes.
In a typical FEA workflow, once the nodal displacements have been computed, the next step is to calculate the displacement field itself, often for visualization purposes, and then to compute stresses using constitutive relationships (e.g., Hooke’s law in the case of linear elasticity). Visualization further aids in identifying regions of high stress or large deformations. Tools like the plotters crate allow Rust to directly generate high-quality plots, which can be used to create graphical representations such as deformation plots, contour maps of stress, and more.
Below is an example implementation in Rust that demonstrates the post-processing steps, including computing the displacement field from a solved nodal displacement vector, calculating stress using a simple linear elastic model, and visualizing the displacement field as a 2D plot.
use nalgebra::{DMatrix, DVector};
use plotters::prelude::*;
use ndarray::Array2;
/// Computes the displacement field from the nodal displacement vector for a 2D problem.
/// The displacement vector `u` is assumed to store values as (u_x1, u_y1, u_x2, u_y2, ...).
/// The function returns a vector of (x, y) displacement tuples.
fn compute_displacement_field(u: &DVector<f64>) -> Vec<(f64, f64)> {
// Process the displacement vector in chunks of 2 (for x and y components).
u.as_slice()
.chunks(2)
.map(|chunk| (chunk[0], chunk[1]))
.collect()
}
/// Computes the stress at an element using Hooke's law for a 2D linear elastic material.
/// Given the nodal displacement vector `u`, the elasticity matrix `C`, and a strain-displacement matrix `B`,
/// this function calculates the strain as ε = B * u and then computes stress as σ = C * ε.
fn compute_stress(u: &DVector<f64>, elasticity_matrix: &DMatrix<f64>, strain_displacement_matrix: &DMatrix<f64>) -> DVector<f64> {
// Calculate strain using the strain-displacement matrix.
let strain = strain_displacement_matrix * u;
// Compute stress by applying the elasticity matrix.
elasticity_matrix * strain
}
/// Plots the 2D displacement field using the plotters crate.
/// The displacement field is provided as a vector of (dx, dy) tuples, and the plot is saved to the specified output file.
fn plot_displacement_field(displacement_field: &[(f64, f64)], output_file: &str) -> Result<(), Box<dyn std::error::Error>> {
// Create a drawing area with specified dimensions.
let root = BitMapBackend::new(output_file, (800, 600)).into_drawing_area();
root.fill(&WHITE)?;
// Calculate a suitable scaling factor for the plot based on maximum displacement magnitude.
let max_disp = displacement_field.iter()
.map(|&(dx, dy)| (dx.powi(2) + dy.powi(2)).sqrt())
.fold(0.0, f64::max);
// Build a chart with the computed plotting area.
let mut chart = ChartBuilder::on(&root)
.caption("Displacement Field", ("sans-serif", 50).into_font())
.margin(10)
.x_label_area_size(30)
.y_label_area_size(30)
.build_cartesian_2d(-max_disp..max_disp, -max_disp..max_disp)?;
chart.configure_mesh().draw()?;
// Plot each displacement as a point.
for &(dx, dy) in displacement_field {
chart.draw_series(PointSeries::of_element(
vec![(dx, dy)],
5, // Size of the point
&BLUE,
&|c, s, st| {
EmptyElement::at(c) + Circle::new((0, 0), s, st.filled())
},
))?;
}
root.present()?;
Ok(())
}
fn main() {
// Example: Assume we have solved an FEA problem and obtained a nodal displacement vector.
// Here we create a dummy displacement vector for a 2D problem with 4 nodes,
// where each node has displacements (u_x, u_y).
// For instance, u = [0.0, 0.0, 0.001, 0.002, 0.002, 0.001, 0.003, 0.004]
// corresponds to nodes with displacements: (0,0), (0.001, 0.002), (0.002, 0.001), (0.003, 0.004).
let u_data = vec![0.0, 0.0, 0.001, 0.002, 0.002, 0.001, 0.003, 0.004];
let u = DVector::from_vec(u_data);
// Compute the displacement field from the nodal displacement vector.
let displacement_field = compute_displacement_field(&u);
// For demonstration, assume a simple elasticity model.
// Define an elasticity matrix C (for plane stress in a linear elastic material)
// and a strain-displacement matrix B for an element. In practice, these matrices depend on the material
// properties and the element geometry. Here we use arbitrary values for illustration.
let elasticity_matrix = DMatrix::from_row_slice(3, 3, &[
210e9, 0.0, 0.0,
0.0, 210e9, 0.0,
0.0, 0.0, 80e9,
]);
let strain_displacement_matrix = DMatrix::from_row_slice(3, 8, &[
0.5, 0.0, -0.5, 0.0, 0.5, 0.0, -0.5, 0.0,
0.0, 0.5, 0.0, -0.5, 0.0, 0.5, 0.0, -0.5,
0.1, 0.1, 0.1, 0.1, -0.1, -0.1, -0.1, -0.1,
]);
// Compute the stress vector for an element using the computed displacements.
let stress = compute_stress(&u, &elasticity_matrix, &strain_displacement_matrix);
println!("Computed stress: \n{}", stress);
// Visualize the displacement field by generating a 2D plot.
// The plot will be saved as "displacement_field.png".
plot_displacement_field(&displacement_field, "displacement_field.png")
.expect("Failed to generate displacement field plot");
println!("Displacement field plot has been generated and saved as 'displacement_field.png'.");
}
In this example, the function compute_displacement_field extracts the (x, y) displacements from a one-dimensional displacement vector for a 2D problem, making it easy to later plot these displacements. The compute_stress function applies Hooke's law in a simplified manner by first calculating the strain from a strain-displacement matrix and then obtaining stress using the elasticity matrix. Finally, plot_displacement_field uses the plotters crate to generate a visual representation of the displacement field. The chart is set up with appropriate scaling and mesh configuration, and each displacement is drawn as a point on the 2D plot.
After computing the displacement field and stress vector, the main function demonstrates their usage and generates a displacement plot saved as an image file. This full post-processing workflow—from computing displacements and stresses to visualizing the results—enables engineers to interpret simulation outcomes effectively.
By leveraging Rust's computational capabilities and integrating with visualization tools, you can ensure that the results of an FEA simulation are both accurate and accessible for analysis. This post-processing phase is crucial in verifying simulation accuracy and in guiding further design improvements or research investigations.
14.8. Advanced Topics
Finite Element Analysis (FEA) is not limited to linear, static problems; many real-world structural challenges involve nonlinear behavior, dynamic loading, and the need to understand vibration characteristics through modal analysis. Nonlinear analysis is necessary when material properties, geometry, or boundary conditions lead to a response that is not directly proportional to the applied loads. For example, large deformations or plasticity create a situation where the stiffness matrix becomes a function of the displacements, requiring iterative solution approaches such as the Newton–Raphson method. Dynamic analysis, by contrast, addresses time-dependent behavior. This requires solving the equations of motion, which typically have the form
$\mathbf{M}\ddot{\mathbf{u}}(t) + \mathbf{C}\dot{\mathbf{u}}(t) + \mathbf{K}\mathbf{u}(t) = \mathbf{F}(t),$
where M\\mathbf{M}, C\\mathbf{C}, and K\\mathbf{K} are the mass, damping, and stiffness matrices, respectively. Time integration methods—such as the Newmark-beta method—are used to solve these equations step-by-step in time.
Modal analysis is essential for understanding a structure’s vibrational characteristics. By solving the generalized eigenvalue problem
$\mathbf{K}\mathbf{\phi} = \lambda \mathbf{M}\mathbf{\phi},$
one can obtain the natural frequencies (related to λ\\lambda) and mode shapes (ϕ\\mathbf{\\phi}). These insights help engineers predict resonance, assess stability under dynamic loads, and design for vibrational performance.
Rust’s performance, memory safety, and powerful numerical libraries make it well-suited for implementing these advanced FEA techniques. The following code examples illustrate how to implement simple routines for nonlinear stiffness updates, dynamic analysis using the Newmark-beta method, and modal analysis using eigenvalue solvers.
Below is an example function that updates the stiffness matrix to account for geometric nonlinearity. In this basic model, the stiffness matrix is modified by adding a term proportional to the product of nodal displacements, simulating a simple form of nonlinearity:
use nalgebra::{DMatrix, DVector};
/// Updates the linear stiffness matrix to account for nonlinearity.
/// This is a simple model in which an extra term, proportional to the product of displacements,
/// is added to each entry of the matrix. The nonlinearity_factor determines the strength of this effect.
fn update_stiffness_matrix(k_linear: &DMatrix<f64>, displacements: &DVector<f64>, nonlinearity_factor: f64) -> DMatrix<f64> {
let mut k_nonlinear = k_linear.clone();
for i in 0..k_nonlinear.nrows() {
for j in 0..k_nonlinear.ncols() {
k_nonlinear[(i, j)] += nonlinearity_factor * displacements[i] * displacements[j];
}
}
k_nonlinear
}
Next, a Newton–Raphson based iterative solver is employed for solving the nonlinear system. This function repeatedly updates the displacement vector until the residual (the difference between the applied load and the internal forces) is below a set tolerance:
/// Solves a nonlinear system of equations representing an FEA problem using the Newton–Raphson method.
/// The function uses the linear stiffness matrix (k_linear), the force vector (f), a convergence tolerance (tol),
/// a maximum number of iterations (max_iter), and a nonlinearity factor to update the stiffness matrix.
/// It returns the computed displacement vector.
fn solve_nonlinear_system(k_linear: DMatrix<f64>, f: DVector<f64>, tol: f64, max_iter: usize, nonlinearity_factor: f64) -> DVector<f64> {
// Start with an initial guess of zero displacements.
let mut u = DVector::zeros(f.len());
for _ in 0..max_iter {
// Update stiffness matrix to account for nonlinearity based on current displacements.
let k_nonlinear = update_stiffness_matrix(&k_linear, &u, nonlinearity_factor);
// Compute the residual: f - K(u) * u.
let residual = &f - &k_nonlinear * &u;
// Check convergence via the norm of the residual.
if residual.norm() < tol {
break;
}
// Solve for the displacement increment using LU decomposition.
let delta_u = k_nonlinear.lu().solve(&residual).expect("Failed to solve during Newton-Raphson iteration.");
u += delta_u;
}
u
}
For dynamic analysis, the Newmark-beta method is used for time integration of the equations of motion. The following function integrates the system over a given number of time steps. It calculates updated displacements, velocities, and accelerations at each time step:
/// Implements the Newmark-beta method for dynamic analysis of an FEA problem.
/// Given the mass matrix (m), damping matrix (c), stiffness matrix (k), external force vector (f),
/// and initial conditions (u0 and v0), this function computes the displacements and velocities over time.
/// beta and gamma are the Newmark method parameters, dt is the time step, and steps is the number of time steps.
fn newmark_beta(
m: &DMatrix<f64>, c: &DMatrix<f64>, k: &DMatrix<f64>, f: &DVector<f64>,
u0: &DVector<f64>, v0: &DVector<f64>, dt: f64, beta: f64, gamma: f64, steps: usize
) -> (DVector<f64>, DVector<f64>) {
let mut u = u0.clone();
let mut v = v0.clone();
// Compute initial acceleration: a0 = M^{-1}*(F - K*u0 - C*v0)
let mut a = m.lu().solve(&(f - k * u0 - c * v0)).expect("Failed to compute initial acceleration");
// Precompute effective stiffness matrix: K_eff = K + (gamma/(beta*dt))*C + (1/(beta*dt^2))*M
let k_eff = k + &(c * (gamma / (beta * dt))) + &(m * (1.0 / (beta * dt * dt)));
for _ in 0..steps {
// Compute effective force vector based on current u, v, and a.
let f_eff = f + m * (u.clone() / (beta * dt * dt) + v.clone() / (beta * dt) + a.clone() * (0.5 / beta - 1.0))
+ c * (gamma / (beta * dt) * u.clone() + (gamma / beta - 1.0) * v.clone() + dt * (gamma / (2.0 * beta) - 1.0) * a.clone());
// Solve for new displacements.
let u_new = k_eff.lu().solve(&f_eff).expect("Failed to solve in Newmark-beta");
// Update velocity and acceleration using the Newmark formulas.
let v_new = (u_new.clone() - u.clone()) * (gamma / (beta * dt)) + v.clone() * (1.0 - gamma / beta) + a.clone() * dt * (1.0 - gamma / (2.0 * beta));
let a_new = (u_new.clone() - u.clone()) / (beta * dt * dt) - v.clone() / (beta * dt) - a.clone() * (0.5 / beta - 1.0);
u = u_new;
v = v_new;
a = a_new;
}
(u, v)
}
The newmark_beta function begins by computing the initial acceleration from the initial displacements and velocities. The effective stiffness matrix is then precomputed and used during each time step to solve for the updated displacement. Finally, velocity and acceleration are updated according to the Newmark-beta formulas.
For modal analysis, which involves solving eigenvalue problems to obtain natural frequencies and mode shapes, the nalgebra crate provides an efficient way to compute eigenvalues and eigenvectors. The following function sets up and solves a generalized eigenvalue problem typical in structural dynamics:
use nalgebra::linalg::SymmetricEigen;
/// Performs modal analysis by solving the generalized eigenvalue problem:
/// K * φ = λ * M * φ
/// where K is the global stiffness matrix, M is the mass matrix, λ are the eigenvalues,
/// and φ are the corresponding mode shapes.
/// This function returns a tuple containing the eigenvalues (which are the natural frequencies squared)
/// and the eigenvectors (the mode shapes).
fn solve_modal_analysis(k: &DMatrix<f64>, m: &DMatrix<f64>) -> (DVector<f64>, DMatrix<f64>) {
// Convert the generalized eigenvalue problem to a standard one using Cholesky decomposition.
// This simplification assumes that M is symmetric and positive-definite.
let cholesky_m = m.cholesky().expect("Mass matrix is not positive definite");
let inv_cholesky = cholesky_m.inverse();
// Transform the stiffness matrix: K' = inv(M^{1/2}) * K * inv(M^{1/2})
let k_transformed = &inv_cholesky.transpose() * k * &inv_cholesky;
// Compute eigenvalues and eigenvectors of the transformed matrix.
let eigen = SymmetricEigen::new(k_transformed);
(eigen.eigenvalues, eigen.eigenvectors)
}
This function first performs a Cholesky decomposition of the mass matrix, then transforms the stiffness matrix into a standard eigenvalue problem, and finally solves for the natural frequencies and mode shapes.
In summary, solving the system of equations arising in FEA requires the selection of an appropriate solver based on the size and nature of the problem. For linear static systems, direct solvers like LU decomposition provide robust solutions, whereas iterative methods such as the Conjugate Gradient method are more suitable for large, sparse systems. Dynamic analysis using time integration methods like Newmark-beta and modal analysis via eigenvalue problems further expand the capability of FEA to address complex, time-dependent, and vibrational problems. Rust’s performance, safety, and extensive numerical libraries make it an excellent choice for implementing and scaling these advanced techniques, ensuring that advanced FEA applications are both robust and efficient.
The code examples provided above offer a foundation upon which more elaborate FEA solvers can be built. As problems increase in complexity, additional methods—such as preconditioning for iterative solvers, adaptive time-stepping, and higher-order element formulations—can be integrated into the Rust framework to further enhance simulation capabilities.
14.9. Performance Optimization
Finite Element Analysis is computationally intensive, especially when applied to large-scale and complex structural problems. In industrial applications like automotive crash simulations or aerospace structural analyses, the number of elements and nodes can reach millions, making it essential to optimize performance to obtain results within reasonable time and resource budgets. Common challenges include the assembly of global stiffness matrices, solving large linear systems, and managing data movement efficiently. Each of these tasks, if not optimized, can become a major bottleneck. Rust’s powerful concurrency model, memory safety, and modern libraries provide the tools needed for such optimizations.
One major performance bottleneck is matrix assembly. In FEA, the global stiffness matrix is built by combining the local stiffness matrices of individual elements. For large models, the resulting matrix is typically sparse, meaning most of its entries are zero. Using dense representations wastes memory and computational power, so it becomes necessary to adopt a sparse matrix representation. Libraries such as the sprs crate in Rust provide data structures designed for sparse matrices, which help in reducing both memory usage and computational cost.
The following code demonstrates how to assemble the global stiffness matrix in parallel using Rayon and a sparse matrix representation via the sprs crate. In this example, each element’s contribution is processed concurrently, and a triplet (coordinate) matrix is built to collect nonzero entries. Finally, the triplet is converted into a sparse Compressed Sparse Row (CSR) matrix.
// Cargo.toml dependencies:
// [dependencies]
// ndarray = "0.15"
// sprs = "0.11"
// rayon = "1.5"
use ndarray::Array2;
use sprs::{CsMat, TriMat};
use rayon::prelude::*;
/// Represents a finite element for a 1D bar with a 2x2 stiffness matrix and node connectivity.
struct Element {
stiffness: Array2<f64>,
nodes: (usize, usize),
}
impl Element {
/// Creates a new Element using Young's modulus (E), cross-sectional area (A), element length, and node connectivity.
/// The stiffness matrix is computed as (E*A/length)*[[1, -1], [-1, 1]].
fn new(E: f64, A: f64, length: f64, nodes: (usize, usize)) -> Self {
let k = E * A / length;
let stiffness = Array2::from_shape_vec((2, 2), vec![k, -k, -k, k]).unwrap();
Element { stiffness, nodes }
}
}
/// Assembles the global stiffness matrix using a sparse matrix approach in parallel.
/// Each element's contributions are added into a triplet (coordinate) matrix concurrently.
/// The final sparse matrix is returned in Compressed Sparse Row (CSR) format.
fn assemble_global_stiffness_parallel(elements: &[Element], num_nodes: usize) -> CsMat<f64> {
// Create a vector to accumulate local triplets in parallel.
let triplets: Vec<TriMat<f64>> = elements.par_iter().map(|element| {
let mut local_triplet = TriMat::new((num_nodes, num_nodes));
let (i, j) = element.nodes;
local_triplet.add_triplet(i, i, element.stiffness[[0, 0]]);
local_triplet.add_triplet(i, j, element.stiffness[[0, 1]]);
local_triplet.add_triplet(j, i, element.stiffness[[1, 0]]);
local_triplet.add_triplet(j, j, element.stiffness[[1, 1]]);
local_triplet
}).collect();
// Create a global triplet matrix and merge contributions from all local triplets.
let mut global_triplet = TriMat::new((num_nodes, num_nodes));
for local_triplet in triplets {
for (val, (row, col)) in local_triplet.triplet_iter() {
global_triplet.add_triplet(row, col, *val); // Dereference val to use the actual value
}
}
// Convert the triplet matrix to CSR format for efficient operations.
global_triplet.to_csr()
}
// Example usage for assembling the global stiffness matrix.
fn main() {
// Define material properties and the geometry for a simple 1D bar problem.
let E = 210e9; // Young's modulus in Pascals (e.g., steel)
let A = 0.01; // Cross-sectional area in square meters
let length = 1.0; // Length of each element in meters
let num_elements = 2;
let num_nodes = num_elements + 1; // Total nodes = elements + 1
// Create elements representing two adjacent 1D bar elements.
let elements = vec![
Element::new(E, A, length, (0, 1)),
Element::new(E, A, length, (1, 2)),
];
// Assemble the global stiffness matrix in a sparse, parallel manner.
let global_stiffness = assemble_global_stiffness_parallel(&elements, num_nodes);
// Display the assembled sparse global stiffness matrix.
println!("Global Stiffness Matrix (Sparse, Parallel):");
println!("{:?}", global_stiffness);
// Further processing, such as solving the system, would follow here.
}
In the code above, each Element is initialized with its local stiffness matrix calculated using the material properties and geometry. The function assemble_global_stiffness_parallel uses Rayon’s parallel iterators to process each element concurrently, adding its contribution to a local triplet matrix. These local contributions are then merged into a global triplet, which is converted into a sparse CSR matrix for efficient storage and subsequent computations. This parallel assembly method can substantially reduce runtime, especially for large-scale problems.
Another critical aspect of performance optimization is solving the system of equations efficiently. For large, sparse systems, iterative solvers like the Conjugate Gradient method are often preferred. Coupled with efficient sparse matrix representations and preconditioning techniques, iterative solvers can offer significant performance improvements over direct methods.
The code examples presented here represent a fraction of the strategies available for performance optimization in FEA. Profiling tools such as cargo-flamegraph can help identify bottlenecks, and Rust’s ownership model ensures that memory is used safely and efficiently, reducing the chance of memory leaks and other errors. By integrating parallel processing, using sparse matrix techniques, and optimizing solver algorithms, FEA applications written in Rust can achieve high performance even when facing the challenges of industrial-scale simulations.
This section demonstrates that with thoughtful design and careful implementation, substantial performance gains can be realized in FEA simulations. Rust’s robust ecosystem provides a strong foundation for developing optimized, scalable, and safe FEA software—capable of tackling some of the most demanding engineering problems.
14.10. Case Studies and Applications
Finite Element Analysis (FEA) has become indispensable across many industries—including civil, mechanical, and aerospace engineering—due to its ability to simulate complex structural behavior and predict the performance of designs under various loading conditions. Whether it is ensuring that bridges can sustain heavy traffic loads, verifying that aircraft structures will not experience resonant vibrations, or analyzing the stress distribution in mechanical components, FEA enables engineers to gain detailed insights into potential failure modes and design improvements before building physical prototypes.
In practical applications, FEA involves important trade-offs. For instance, achieving higher accuracy often requires finer meshes, more sophisticated material models, and extended iteration cycles, which lead to increased computational cost and longer simulation times. Conversely, in time-sensitive or preliminary design studies, engineers may opt for coarser meshes or simplified models—sacrificing some degree of accuracy for reduced solution time. The optimal balance between cost and fidelity is determined by the specific requirements of the project.
To illustrate how FEA can be applied to solve real-world problems, we present a case study of a simple 2D truss bridge model. In this example, the bridge is subjected to vertical loads that represent the weight of vehicles passing over it. The objective is to determine the nodal displacements and compute the stress in each truss element. This case study highlights the implementation challenges, such as defining the geometry, applying appropriate boundary conditions, assembling the global stiffness matrix, and solving the system of equations.
Below is a Rust implementation using the nalgebra crate for matrix operations. The model defines a TrussElement representing a single element of the truss and a TrussStructure that includes the connectivity of the nodes, the applied supports, and the loads. Each truss element calculates its local stiffness matrix based on its material properties (Young's modulus), cross-sectional area, and element length. The TrussStructure then assembles the global stiffness matrix by summing contributions from all elements, applies support boundary conditions, and solves the system to obtain nodal displacements.
use nalgebra::{DMatrix, DVector};
struct TrussElement {
node_start: usize,
node_end: usize,
area: f64,
young_modulus: f64,
}
/// 2D truss structure
struct TrussStructure {
elements: Vec<TrussElement>,
nodes: Vec<(f64, f64)>,
supports: Vec<usize>,
loads: Vec<(usize, f64)>, // (node, vertical load)
}
impl TrussElement {
/// Returns the 4x4 element stiffness matrix in global coordinates.
fn stiffness_matrix_2d(&self, nodes: &[(f64, f64)]) -> DMatrix<f64> {
let (x1, y1) = nodes[self.node_start];
let (x2, y2) = nodes[self.node_end];
let dx = x2 - x1;
let dy = y2 - y1;
let length = (dx*dx + dy*dy).sqrt();
let c = dx / length;
let s = dy / length;
let k = self.young_modulus * self.area / length;
// 4x4
DMatrix::from_row_slice(4, 4, &[
k * c * c, k * c * s, -k * c * c, -k * c * s,
k * c * s, k * s * s, -k * c * s, -k * s * s,
-k * c * c, -k * c * s, k * c * c, k * c * s,
-k * c * s, -k * s * s, k * c * s, k * s * s,
])
}
}
impl TrussStructure {
/// Assemble the global stiffness matrix (2*N x 2*N).
fn global_stiffness_matrix(&self) -> DMatrix<f64> {
let num_nodes = self.nodes.len();
let mut k_global = DMatrix::<f64>::zeros(2 * num_nodes, 2 * num_nodes);
for element in &self.elements {
let k_e = element.stiffness_matrix_2d(&self.nodes);
let i = element.node_start;
let j = element.node_end;
// DOFs
let dofs_i = [2*i, 2*i+1];
let dofs_j = [2*j, 2*j+1];
// Place k_e into K_global
// local rows 0-> i_x, 1-> i_y, 2-> j_x, 3-> j_y
let map = [dofs_i[0], dofs_i[1], dofs_j[0], dofs_j[1]];
for (r_local, r_global) in map.iter().enumerate() {
for (c_local, c_global) in map.iter().enumerate() {
k_global[(*r_global, *c_global)] += k_e[(r_local, c_local)];
}
}
}
k_global
}
/// Zero rows/columns for supported DOFs, set diag=1, enforce 0 in force vector.
fn apply_boundary_conditions(&self, k_global: &mut DMatrix<f64>, f_global: &mut DVector<f64>) {
for &support in &self.supports {
// x dof = 2*support, y dof = 2*support+1
for i in 0..2 {
let dof = 2*support + i;
// zero row and col
for j in 0..k_global.nrows() {
k_global[(dof, j)] = 0.0;
k_global[(j, dof)] = 0.0;
}
k_global[(dof, dof)] = 1.0;
f_global[dof] = 0.0;
}
}
}
}
fn solve_truss_structure(structure: &TrussStructure) -> DVector<f64> {
let mut k_global = structure.global_stiffness_matrix();
let mut f_global = DVector::<f64>::zeros(2 * structure.nodes.len());
// Apply vertical loads
for &(n, load_val) in &structure.loads {
let dof_y = 2*n + 1; // Y dof
f_global[dof_y] += load_val;
}
structure.apply_boundary_conditions(&mut k_global, &mut f_global);
// Solve
k_global.lu().solve(&f_global)
.expect("Failed to solve the truss structure system")
}
/// Compute axial stress in each element
fn compute_stress(structure: &TrussStructure, disp: &DVector<f64>) -> Vec<f64> {
let mut result = Vec::with_capacity(structure.elements.len());
for e in &structure.elements {
let (x1, y1) = structure.nodes[e.node_start];
let (x2, y2) = structure.nodes[e.node_end];
let dx = x2 - x1;
let dy = y2 - y1;
let length = (dx*dx + dy*dy).sqrt();
let c = dx / length;
let s = dy / length;
// Displacements
let u1 = disp[2*e.node_start];
let v1 = disp[2*e.node_start + 1];
let u2 = disp[2*e.node_end];
let v2 = disp[2*e.node_end + 1];
// Project the displacement difference on the element axis
let strain = ((u2 - u1)*c + (v2 - v1)*s) / length;
let stress = e.young_modulus * strain;
result.push(stress);
}
result
}
fn main() {
// Example: 3 nodes in a "bridge" shape
let nodes = vec![
(0.0, 0.0), // Node 0
(5.0, 1.0), // Node 1
(10.0, 0.0), // Node 2
];
// Elements: 0-1, 1-2
let elements = vec![
TrussElement {
node_start: 0,
node_end: 1,
area: 0.005,
young_modulus: 210e9,
},
TrussElement {
node_start: 1,
node_end: 2,
area: 0.005,
young_modulus: 210e9,
},
];
// Supports at nodes 0 and 2
let supports = vec![0, 2];
// Vertical load at node 1
let loads = vec![(1, -1000.0)];
let structure = TrussStructure {
elements,
nodes,
supports,
loads,
};
let displacements = solve_truss_structure(&structure);
println!("Nodal Displacements =\n{:?}", displacements);
let stresses = compute_stress(&structure, &displacements);
for (i, s) in stresses.iter().enumerate() {
println!("Stress in Element {} = {:.3e} Pa", i, s);
}
}
In this example, we first define the nodes, elements, supports, and loads for a simplified 2D truss bridge. The TrussElement struct contains the basic properties of each element, while the TrussStructure struct holds the overall model data. The method global_stiffness_matrix assembles the global stiffness matrix from the contributions of individual elements, and apply_boundary_conditions enforces the support conditions. The function solve_truss_structure assembles the force vector, applies boundary conditions, and solves the system Ku=F\\mathbf{K} \\mathbf{u} = \\mathbf{F} using LU decomposition. Finally, the stress in each element is computed based on the difference in nodal displacements.
This case study demonstrates how FEA can be practically applied to solve real-world engineering problems, such as assessing the structural integrity of a bridge under load. It also illustrates the trade-offs involved in FEA applications—balancing model accuracy, computational cost, and solution time. Rust’s performance, safety, and strong ecosystem of numerical libraries make it particularly well-suited for developing robust FEA applications capable of addressing complex industrial challenges.
14.11. Conclusion
Chapter 14 equips readers with the essential knowledge and practical skills to implement Finite Element Analysis for structural mechanics using Rust. By the end of this chapter, readers will have a deep understanding of FEA, from foundational principles to advanced applications, and be prepared to tackle a wide range of structural mechanics challenges with confidence and precision. This chapter bridges the gap between theory and practice, ensuring that readers are not just passive learners but active practitioners in the field of computational physics.
14.11.1. Further Learning with GenAI
The following prompts are designed to help you delve deeply into the intricacies of Finite Element Analysis (FEA) for Structural Mechanics using Rust. These questions cover a range of topics from the fundamental principles and mathematical foundations of FEA to advanced topics such as nonlinear analysis, performance optimization, and practical applications.
Describe the evolution of Finite Element Analysis (FEA) from its inception to its current role in structural mechanics, emphasizing the key breakthroughs and technological advancements that have shaped its development. How has the integration of modern programming languages like Rust influenced the efficiency, accuracy, and scalability of FEA in computational physics? Provide examples of specific Rust features that enhance FEA implementations.
Discuss the process of discretizing a continuous domain into finite elements within the context of FEA. How do the choices of node placement, element type, and meshing strategy impact the accuracy and computational cost of the analysis? Explain how these concepts are implemented in Rust, including examples of potential trade-offs between accuracy and computational efficiency.
Examine the mathematical foundations of FEA, focusing on the role of differential equations and variational principles in deriving the stiffness matrix. How does the weak form of the governing equations facilitate the numerical solution of structural mechanics problems? Illustrate how these mathematical concepts are translated into Rust code, with detailed explanations of each step, including the use of specific Rust libraries or features.
Walk through the process of deriving the weak form of a boundary value problem for a structural mechanics scenario. How does the Galerkin method ensure that the solution satisfies the governing equations in an approximate sense? Provide a Rust implementation of this process, highlighting the critical decisions made during coding and their impact on the solution's accuracy and convergence.
Discuss the various mesh generation techniques used in FEA and their implications for solution quality and computational efficiency. How do different element types (1D, 2D, 3D) influence the interpolation accuracy and convergence of the FEA solution? Provide a comprehensive analysis of implementing mesh generation and element connectivity in Rust, with examples of handling complex geometries and ensuring numerical stability.
Explore the role of shape functions in FEA, particularly in the context of interpolating field variables within elements. How do higher-order shape functions compare to linear ones in terms of accuracy and computational cost? Demonstrate how to implement different types of shape functions in Rust, including examples of their application to specific structural mechanics problems, and discuss the trade-offs involved in choosing different orders of shape functions.
Explain the assembly process of the global stiffness matrix in FEA, detailing how individual element stiffness matrices are combined to form the system of equations. What optimization strategies can be employed to handle large-scale problems efficiently? Provide a Rust implementation of the assembly process, including techniques for sparse matrix representation and memory management, and discuss the impact of these optimizations on performance.
Compare and contrast direct and iterative solvers in the context of solving linear systems arising from FEA. What are the advantages and disadvantages of each approach in terms of computational efficiency, scalability, and accuracy? Provide Rust implementations of both types of solvers, along with a performance analysis that highlights the scenarios in which each solver type is most effective.
Discuss the importance of preconditioning in improving the convergence of iterative solvers in FEA. What are the most commonly used preconditioning techniques, and how do they enhance the performance of solvers like the Conjugate Gradient method? Provide a detailed example of implementing a preconditioner in Rust, and analyze its impact on the convergence rate and computational efficiency in a structural mechanics problem.
Explore the role of boundary conditions in FEA, focusing on how they influence the solution of structural mechanics problems. What are the challenges associated with implementing different types of boundary conditions (Dirichlet, Neumann) in FEA, and how can these be addressed in Rust? Provide examples of Rust functions for applying boundary conditions, with a discussion on how to handle complex or mixed boundary conditions in real-world scenarios.
Explain the significance of post-processing in FEA, particularly in interpreting results like stress, strain, and displacement fields. How can post-processing techniques be implemented in Rust to efficiently compute and visualize these results? Provide examples of integrating Rust with visualization tools for displaying FEA results, and discuss the challenges of ensuring accurate and meaningful interpretations of the data.
Discuss the challenges of performing nonlinear analysis in FEA, particularly when dealing with geometric and material nonlinearities. How can Rust be used to implement a nonlinear solver for structural mechanics, and what techniques can be employed to ensure convergence and stability? Provide a detailed example of a nonlinear analysis in Rust, including the implementation of iterative solvers and the handling of large deformations.
Explore the importance of dynamic analysis in FEA, focusing on how time integration methods like Newmark-beta are used to simulate the dynamic response of structures. How can these methods be implemented in Rust, and what considerations must be made to ensure stability and accuracy? Provide an example of a dynamic FEA simulation in Rust, discussing the choice of time step and integration method.
Examine the process of modal analysis in FEA, including its use in assessing the dynamic behavior of structures through the calculation of natural frequencies and mode shapes. How can eigenvalue problems be solved efficiently in Rust, and what are the key factors that influence the accuracy of modal analysis? Provide a detailed implementation of modal analysis in Rust, including the use of numerical libraries for eigenvalue computation.
Discuss the key strategies for optimizing FEA implementations for large-scale problems, with a focus on computational efficiency and memory management. How can Rust's concurrency features be leveraged to parallelize FEA computations and improve performance? Provide examples of Rust code that demonstrate parallel processing in FEA, including the use of libraries like Rayon for handling large datasets and complex calculations.
Explore the application of parallel computing techniques in FEA, particularly in the context of handling large-scale simulations and complex structural mechanics problems. How can Rust's parallelism libraries be integrated into FEA workflows to enhance computational efficiency? Provide detailed examples of parallelizing FEA tasks in Rust, with a discussion on the challenges and benefits of parallel computing in this domain.
Analyze a specific real-world case study where FEA was used to solve a complex structural mechanics problem. How can this problem be implemented in Rust, and what are the key challenges and considerations involved in setting up and solving the problem? Provide a step-by-step guide to implementing the case study in Rust, including the modeling, solution, and post-processing phases.
Explore advanced topics in FEA, such as multi-scale modeling, adaptive mesh refinement, and coupled multi-physics simulations. How can these advanced techniques be implemented in Rust to improve the accuracy and efficiency of FEA simulations? Provide examples of Rust code that demonstrate these advanced techniques, with a discussion on their application to complex engineering problems.
Discuss the emerging trends and future directions in FEA, particularly in the context of high-performance computing, cloud-based simulations, and the integration of machine learning techniques. How can Rust be positioned as a key tool in advancing these developments, and what are the potential benefits of using Rust in cutting-edge FEA research? Provide a forward-looking analysis of the role of Rust in the future of FEA, including examples of how Rust can be used to implement next-generation FEA techniques.
Provide an in-depth exploration of the ethical and practical considerations involved in using FEA for critical structural mechanics applications, such as in aerospace, civil engineering, and infrastructure safety. How can Rust be used to ensure the reliability, accuracy, and transparency of FEA simulations in these high-stakes environments? Discuss the role of validation, verification, and certification in FEA, with examples of how Rust can support these processes.
Each prompt challenges you to explore the nuances of FEA, from foundational principles to advanced applications, pushing the boundaries of what you can achieve in computational physics. Your journey through these topics will empower you to contribute meaningfully to the field of structural analysis and computational mechanics.
14.11.2. Assignments for Practice
Each exercise focuses on practical applications and challenges, providing you with the opportunity to implement and test key FEA concepts. Through these exercises, you will develop a deeper understanding of how to apply Rust in computational physics, optimize performance, and address real-world structural analysis problems effectively.
Exercise 14.1: Discretization and Mesh Generation
Task: Develop a comprehensive Rust program to generate a mesh for a 2D structural problem involving a rectangular domain. The mesh should consist of triangular elements, and the program should include the following features:
Functionality for creating and refining the mesh.
Integration of different types of triangular elements (e.g., linear, quadratic).
A visualization module to display the mesh structure and verify the accuracy of the discretization.
Objective: Deepen your understanding of mesh generation and discretization techniques in finite element analysis (FEA). Learn to implement and test different types of elements and verify mesh quality through visualization.
Exercise 14.2: Stiffness Matrix Assembly
Task: Implement a Rust function to construct the global stiffness matrix for a 2D structural mechanics problem using a given mesh. This exercise should cover:
Calculation of element stiffness matrices for triangular elements.
Assembling these matrices into the global stiffness matrix, accounting for boundary conditions and node connectivity.
Handling different types of boundary conditions (Dirichlet, Neumann) and applying them in the assembly process.
Testing and validating the matrix assembly with different mesh configurations and boundary conditions.
Objective: Gain hands-on experience in assembling the global stiffness matrix and managing boundary conditions. Understand how to address challenges in matrix assembly and validate results through practical implementation.
Exercise 14.3: Solver Implementation
Task: Create Rust implementations for both a direct solver (e.g., Gaussian elimination with partial pivoting) and an iterative solver (e.g., Conjugate Gradient method) for solving the linear system of equations from FEA. Your implementation should:
Include matrix factorization and solving routines for the direct solver.
Implement iterative methods with convergence criteria and preconditioning techniques.
Compare performance metrics such as computation time and accuracy between the two solvers for varying problem sizes and complexities.
Document the results, discussing trade-offs and suitability for different types of problems.
Objective: Develop and compare direct and iterative solvers for FEA linear systems, enhancing your understanding of their respective performance characteristics and practical applications.
Exercise 14.4: Post-Processing and Visualization
Task: Design a Rust program for post-processing FEA results to extract and analyze stress and strain fields. The program should:
Include functionalities to compute derived quantities such as maximum stress, strain energy, and deformed shapes.
Integrate with a visualization library (e.g., plotting libraries or GUI frameworks) to generate plots and graphical representations of the results.
Implement functionality to handle different types of structural problems (e.g., static, dynamic) and visualize results accordingly.
Evaluate the effectiveness of the visualization in conveying the results and providing insights into the structural behavior.
Objective: Practice post-processing techniques and effective visualization of FEA results. Understand how to present complex data in a meaningful way and assess the impact of visualization on result interpretation.
Exercise 14.5: Nonlinear Analysis Implementation
Task: Develop a Rust-based FEA solver capable of handling nonlinearities, such as material nonlinearity (e.g., plasticity) or geometric nonlinearity (e.g., large deformations). This exercise should:
Implement algorithms for updating stiffness matrices and handling nonlinear behavior during iterations.
Include methods for convergence checking and adaptive step sizing in the solution process.
Test the solver with sample problems exhibiting nonlinear behavior, such as a beam undergoing large deflections or a material undergoing plastic deformation.
Document challenges faced, solutions implemented, and performance metrics for the nonlinear solver.
Objective: Gain experience in extending FEA capabilities to handle nonlinearities, addressing the complexity of nonlinear analysis and enhancing your skills in managing advanced structural problems.
By tackling each challenge, you will build practical skills and a robust understanding of FEA principles, from mesh generation and matrix assembly to solver implementation and nonlinear analysis. These experiences will not only deepen your knowledge but also equip you with the tools to address complex structural problems in computational physics.
Comments