Chapter 6
Finite Difference and Finite Element Methods
“Mathematics is the language in which God has written the universe.” – Galileo Galilei
Chapter 6 of CPVR delves into Finite Difference and Finite Element Methods, providing a comprehensive guide to their implementation using Rust. It begins with an introduction to finite difference methods, explaining discretization, difference formulas, and stability criteria, and continues with a detailed exploration of finite element methods, including the formulation of weak forms, matrix assembly, and application to physical problems. The chapter covers numerical linear algebra techniques essential for solving systems of equations, error analysis and validation practices, and advanced topics such as adaptive methods and parallel computing. The practical aspects emphasize Rust’s capabilities for efficient numerical computation, matrix operations, and performance optimization through concurrency.
6.1. Introduction to Finite Difference Methods
In computational physics, finite difference, finite element, finite volume, and boundary element methods are numerical techniques used to approximate solutions to partial differential equations (PDEs) that describe physical phenomena. Finite difference methods approximate derivatives by using differences between function values at discrete grid points, making them simple and efficient for structured grids. Finite element methods divide the domain into smaller, irregularly shaped elements and use piecewise polynomial functions to approximate the solution, offering flexibility for complex geometries. Finite volume methods, commonly used in fluid dynamics, integrate conservation laws over control volumes, ensuring that fluxes are conserved at the boundaries of each volume, making them well-suited for systems with strong conservation properties. Boundary element methods reduce the dimensionality of the problem by solving only on the boundary of the domain, often leading to computational savings when the physics are defined by boundary conditions, such as in electrostatics or acoustics. Each method has strengths depending on the complexity of the geometry, the conservation properties, and the type of equations being solved.
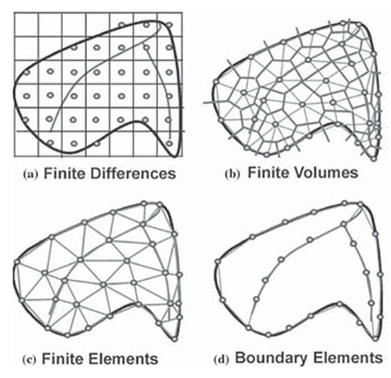
Illustration of finite difference, volumes, elements and boundary elements.
Finite Difference Methods (FDM) are a foundational numerical technique used extensively in computational physics to approximate solutions of partial differential equations (PDEs). In contrast to analytical solutions, which are often unavailable for complex physical systems, FDM replaces continuous derivatives with discrete approximations at grid points. This method involves discretizing the continuous domain—whether spatial, temporal, or both—into a finite set of points where the physical properties of the system are computed.
The discretization process subdivides a continuous domain into a grid. For a one-dimensional (1D) problem, a line segment is divided into evenly spaced points; in two dimensions (2D), a rectangular domain is broken into a mesh of small squares or rectangles. Once the domain is discretized, derivatives that appear in the governing differential equations can be approximated using finite difference formulas. For example, the first derivative of a function u(x)u(x)u(x) at a grid point xix_ixi can be approximated by the forward difference formula:
$$\frac{du}{dx} \approx \frac{u(x_{i+1}) - u(x_i)}{\Delta x}$$
where $\Delta x$ is the distance between adjacent grid points. Similarly, the second derivative can be approximated using the central difference formula:
$$\frac{d^2u}{dx^2} \approx \frac{u(x_{i+1}) - 2u(x_i) + u(x_{i-1})}{\Delta x^2}$$
These approximations are then used to convert the differential equation into a set of algebraic equations, which can be solved using numerical methods.
Stability, consistency, and convergence are critical criteria when using FDM. Stability refers to the property that errors do not grow uncontrollably as the computation progresses. Consistency ensures that the difference equations accurately represent the original differential equations as the grid spacing approaches zero. Convergence guarantees that the numerical solution approaches the exact solution as the grid is refined.
Key properties to consider when using FDM are stability, consistency, and convergence:
Stability ensures that errors—no matter how small—do not grow uncontrollably through successive iterations.
Consistency means that as the grid spacing Δx\\Delta xΔx approaches zero, the difference equations converge toward the original differential equations.
Convergence guarantees that the numerical solution approaches the exact solution as the grid is refined.
Finite difference methods are often divided into explicit and implicit categories:
Explicit Methods: In these methods, the solution at the next time step (or grid point) is computed directly from the values at the current step. They are generally simpler to implement but may require very small time steps to maintain stability.
Implicit Methods: In these methods, the solution at the next step is defined in terms of both known and unknown values, leading to systems of equations that must be solved simultaneously. Implicit methods tend to offer better stability, allowing for larger time steps, but at the cost of increased computational complexity.
Below are two simple examples illustrating the finite difference method applied to steady-state heat conduction problems—a classical boundary value problem.
1D Steady-State Heat Equation
In this example, we approximate the temperature distribution along a rod with fixed temperatures at its ends (Dirichlet boundary conditions). Each interior grid point’s temperature is computed as the average of its two neighboring points.
fn main() {
let n = 10; // Number of grid points along the rod
// Initialize a vector to hold the temperature values
let mut u = vec![0.0; n];
let left_boundary = 100.0; // Temperature at the left end of the rod
let right_boundary = 50.0; // Temperature at the right end of the rod
// Apply boundary conditions
u[0] = left_boundary;
u[n - 1] = right_boundary;
// Apply the finite difference scheme for the interior points
for i in 1..n - 1 {
u[i] = (u[i - 1] + u[i + 1]) / 2.0;
}
// Print the temperature distribution along the rod
for (i, &temp) in u.iter().enumerate() {
println!("u[{}] = {}", i, temp);
}
}
In this example, we create a simple 1D grid with n grid points, representing the temperature distribution along a rod. The boundary conditions are applied at the ends of the grid, with fixed temperatures of 100.0 and 50.0 degrees at the left and right boundaries, respectively.
The finite difference scheme approximates the temperature at each interior grid point using the average of the neighboring points. This is a simple iterative approach that reflects the steady-state solution of the heat equation, where the temperature at any point is the average of its neighbors.
2D Steady-State Heat Equation
For a two-dimensional problem, we create a grid representing the temperature distribution in a rectangular domain. The boundary conditions are applied along all edges, and each interior grid point’s temperature is updated as the average of its four immediate neighbors.
fn main() {
let nx = 10; // Number of grid points in the x-direction
let ny = 10; // Number of grid points in the y-direction
// Create a 2D grid (vector of vectors) for the temperature values
let mut u = vec![vec![0.0; ny]; nx];
let top_boundary = 100.0;
let bottom_boundary = 0.0;
let left_boundary = 75.0;
let right_boundary = 50.0;
// Apply boundary conditions along the vertical edges
for i in 0..nx {
u[i][0] = bottom_boundary;
u[i][ny - 1] = top_boundary;
}
// Apply boundary conditions along the horizontal edges
for j in 0..ny {
u[0][j] = left_boundary;
u[nx - 1][j] = right_boundary;
}
// Apply the finite difference scheme to update interior grid points:
// Each interior point is set to the average of its neighbors
for i in 1..nx - 1 {
for j in 1..ny - 1 {
u[i][j] = (u[i - 1][j] + u[i + 1][j] + u[i][j - 1] + u[i][j + 1]) / 4.0;
}
}
// Print the resulting 2D temperature distribution
for row in u.iter() {
for &temp in row.iter() {
print!("{:>8.2} ", temp);
}
println!();
}
}
In this 2D example, the grid represents a rectangular domain where the temperature is computed at each grid point. The boundary conditions are applied to the edges of the grid, with different temperatures on each boundary. The finite difference scheme here takes the average of the four neighboring points (up, down, left, right) to compute the temperature at each interior point.
This simple iterative approach is an example of an explicit method, where the temperature at each point is updated directly based on the neighboring points. More sophisticated methods, like implicit schemes, would involve solving a system of linear equations, which can be implemented using Rust's array and iterator features or external libraries for more efficient computation.
In practice, handling boundary conditions correctly is crucial for obtaining accurate solutions. Boundary conditions can be Dirichlet (fixed values), Neumann (fixed derivative values), or Robin (a combination of both). Implementing these in Rust requires careful consideration of how to apply the conditions at the grid's edges while iterating through the interior points.
For more complex differential equations or larger grids, direct iterative schemes might become inefficient. In such cases, solver algorithms like Gauss-Seidel, Successive Over-Relaxation (SOR), or Conjugate Gradient methods might be more appropriate. These algorithms can be implemented in Rust using its robust looping constructs and memory management features, allowing for efficient and stable computation of solutions even in large-scale simulations.
In conclusion, the Finite Difference Method is a powerful tool in computational physics, and Rust provides the necessary features to implement these methods effectively. By discretizing the domain, applying difference formulas, and managing boundary conditions, Rust allows for the development of efficient and accurate numerical simulations that are essential for solving complex physical problems.
6.2. Introduction to Finite Element Methods
In computational physics, finite difference (FDM) and finite element (FEM) methods are widely used for solving partial differential equations (PDEs), but they differ significantly in handling geometry and their approach to the solution process. In finite difference methods, the domain is typically represented by a structured grid of points, making it most suitable for regular geometries. In the preprocessing phase, derivatives in the PDE are approximated using differences between neighboring grid points. The resulting algebraic equations are solved numerically. In finite element methods, the domain is discretized into smaller, irregular elements, allowing for flexibility in modeling complex geometries. The preprocessing phase involves meshing the domain and assigning boundary conditions and material properties. In FEM, the PDE is transformed into a variational form, where the solution is approximated using polynomial functions over each element. Both methods then solve the resulting system of algebraic equations numerically, though FEM often involves solving sparse matrix systems. In the post-processing phase, both FDM and FEM methods interpolate the results across the domain, but FEM offers greater precision and flexibility, especially for complex geometries and variable material properties, while FDM is simpler and more efficient for regular grids.
Development life cycle of FDM and FEM methods.
Finite Element Methods (FEM) are a powerful numerical technique for solving partial differential equations (PDEs) over complex geometries. The fundamental idea behind FEM is to discretize the problem domain into smaller, manageable subdomains called finite elements. These elements are typically simple shapes like triangles or quadrilaterals in 2D, or tetrahedra and hexahedra in 3D. The solution to the PDE is then approximated by a piecewise function defined over these elements.
Each finite element is associated with a set of nodes, and the solution is typically approximated by a linear combination of basis functions, also known as shape functions, defined on these nodes. The choice of element shapes and the corresponding shape functions are crucial in determining the accuracy and efficiency of the FEM.
For example, in a 2D problem, the domain might be discretized into a mesh of triangles. For each triangle, the shape functions are defined to interpolate the solution within the element based on the values at the vertices. The global solution is obtained by assembling the contributions from all elements, ensuring continuity across element boundaries.
A critical step in FEM is the formulation of the weak form of the differential equation. The weak form is derived from the strong form (the original PDE) by multiplying it by a test function and integrating over the domain. This process reduces the differentiability requirements on the solution and converts the PDE into an integral equation.
The weak form is essential because it allows the use of piecewise polynomial approximations (which may not be differentiable) for the solution. The result is a set of algebraic equations that can be solved numerically.
For instance, consider the Poisson equation, which is a common PDE in physics:
$$-\nabla^2 u = f \quad \text{in} \quad \Omega$$
with boundary conditions on the domain boundary ∂Ω\\partial \\Omega∂Ω. The weak form of this equation is:
$$\int_{\Omega} \nabla v \cdot \nabla u \, d\Omega = \int_{\Omega} v \, f \, d\Omega \quad \forall v \in V$$
where $v$ is the test function and $V$ is the space of test functions.
In FEM, the weak form leads to a system of linear equations. For linear problems, this system can be expressed in matrix form as:
$$ K \mathbf{u} = \mathbf{f} $$
where $K$ is the global stiffness matrix, $\mathbf{u}$ is the vector of unknowns (e.g., nodal displacements in structural problems), and $\mathbf{f}$ is the force vector. The stiffness matrix $K$ and force vector $\mathbf{f}$ are assembled from the contributions of each element, integrating the shape functions over the domain.
This assembly process involves looping over all elements, calculating the element stiffness matrices and force vectors, and then assembling them into the global system. Boundary conditions are applied to modify the global system, ensuring that the solution satisfies the prescribed constraints.
FEM can be applied to both linear and nonlinear problems. In linear FEM, the relationship between the unknowns (e.g., displacements) and the forces is linear, leading to a linear system of equations as shown above. This linear system can be solved efficiently using direct solvers (like LU decomposition) or iterative solvers (like Conjugate Gradient).
Nonlinear FEM arises when the problem involves nonlinear material properties, large deformations, or nonlinear boundary conditions. In such cases, the stiffness matrix $K$ depends on the unknowns $\mathbf{u}$, leading to a system of nonlinear equations:
$$K(\mathbf{u}) \mathbf{u} = \mathbf{f}(\mathbf{u})$$
This nonlinear system is typically solved using iterative methods such as Newton-Raphson, where the solution is updated iteratively until convergence.
FEM is widely used in structural mechanics for analyzing stresses and deformations in solid structures and in fluid dynamics for simulating the flow of fluids. The versatility of FEM in handling complex geometries and material behaviors makes it an indispensable tool in these fields.
Implementing FEM in Rust involves defining element shape functions, performing numerical integration, assembling the global stiffness matrix and force vector, and solving the resulting system of equations.
Finite element methods (FEM) use several key techniques to approximate solutions to partial differential equations over complex domains. Two fundamental components in FEM are the definition of element shape functions and the numerical integration schemes employed to compute the element matrices, as well as the assembly of these contributions into a global system that can be solved to obtain the approximate solution. In this section, we illustrate how these concepts can be implemented in Rust.
1. Element Shape Functions and Integration Schemes
Shape functions are used to interpolate the solution within an element. For a triangular element in 2D, linear shape functions can be defined as:
$$N_1(\xi, \eta) = 1 - \xi - \eta, \quad N_2(\xi, \eta) = \xi, \quad N_3(\xi, \eta) = \eta$$
Numerical integration techniques, such as Gaussian quadrature, are then used to evaluate integrals over the element. For a triangular element, a simple 2-point or 3-point Gaussian quadrature rule might be applied. One way to represent the integration points and their corresponding weights in Rust is:
// Returns an array of 3 tuples, where each tuple contains (xi, eta, weight)
fn gauss_points() -> [(f64, f64, f64); 3] {
[
(1.0 / 6.0, 1.0 / 6.0, 1.0 / 6.0),
(4.0 / 6.0, 1.0 / 6.0, 1.0 / 6.0),
(1.0 / 6.0, 4.0 / 6.0, 1.0 / 6.0),
]
}
These quadrature points and weights are then used to integrate the element’s stiffness matrix and load vector accurately.
2. Assembly of the Global System
Once local contributions (e.g., the stiffness matrix of an element) are computed using shape functions and integration, they must be assembled into the global stiffness matrix. Each element contributes to certain rows and columns corresponding to its node indices. A more robust approach for assembling the global matrix in Rust is to first represent the element connectivity as an array of node indices per element and then loop over these indices to add the local stiffness contributions to the global system. For example:
// Example placeholder for computing the local stiffness matrix for an element
fn compute_element_stiffness() -> [[f64; 3]; 3] {
// In a real implementation, this function would use the shape functions and gauss_points
// to calculate the 3x3 stiffness matrix for the element.
[[1.0, -0.5, -0.5], [-0.5, 1.0, -0.5], [-0.5, -0.5, 1.0]]
}
/// Assembles the global stiffness matrix from element-level contributions.
/// `elements` is a slice of elements represented as tuples of node indices (e.g., (n1, n2, n3)).
fn assemble_global_matrix(
n_nodes: usize,
elements: &[(usize, usize, usize)],
stiffness: &mut Vec<Vec<f64>>,
) {
for &(n1, n2, n3) in elements.iter() {
let element_nodes = [n1, n2, n3];
let local_stiffness = compute_element_stiffness();
// Assemble the local stiffness matrix into the global stiffness matrix.
for i in 0..3 {
for j in 0..3 {
// Note: this code assumes that 'stiffness' is a square matrix of size n_nodes x n_nodes.
stiffness[element_nodes[i]][element_nodes[j]] += local_stiffness[i][j];
}
}
}
}
In this example, each element is associated with three node indices. The function assemble_global_matrix loops through every element and distributes its local stiffness matrix into the corresponding entries in the global stiffness matrix.
3. Solving the Linear System
Once the global stiffness matrix KK and the load vector f\\mathbf{f} are assembled, the next step is to solve the linear system:
Ku=fK \\mathbf{u} = \\mathbf{f}
The nalgebra crate provides robust tools for matrix operations, including solving linear systems using various decomposition methods. For example, you can solve the system using LU decomposition:
use nalgebra::{DMatrix, DVector};
fn solve_linear_system(k: DMatrix<f64>, f: DVector<f64>) -> DVector<f64> {
// LU decomposition is used to solve the linear system.
// The unwrap() call assumes that the system is solvable.
k.lu().solve(&f).unwrap()
}
This function converts your global stiffness matrix and load vector into DMatrix and DVector types, respectively, from nalgebra and then solves the system to yield the solution vector u\\mathbf{u}.
4. Visualization and Post-Processing
Once the system is solved, it is often useful to visualize and post-process the results, such as plotting the deformed mesh or stress distribution. Rust has crates like plotters for basic visualization, or you can export the numerical data for use with more specialized software like ParaView. The following snippet demonstrates how to use the plotters crate to create a simple plot of a solution vector:
use plotters::prelude::*;
fn plot_results(u: &[f64]) {
// Create a drawing area and output a PNG file.
let root = BitMapBackend::new("results.png", (640, 480)).into_drawing_area();
root.fill(&WHITE).unwrap();
let mut chart = ChartBuilder::on(&root)
.caption("FEM Results", ("sans-serif", 50).into_font())
.build_cartesian_2d(0..u.len(), 0f64..*u.iter().max_by(|a, b| a.partial_cmp(b).unwrap()).unwrap())
.unwrap();
chart.draw_series(LineSeries::new(
u.iter().enumerate().map(|(i, &v)| (i, v)),
&RED,
)).unwrap();
}
fn main() {
// Example solution vector; in practice, this would be the displacement or temperature vector obtained from solving the FEM system.
let u = vec![0.0, 0.5, 1.2, 0.9, 0.7, 0.5, 0.3, 0.2, 0.1, 0.0];
plot_results(&u);
}
In this code, the plot_results function creates a plot showing the variation of the solution vector u\\mathbf{u} across its indices. The drawing area is created using BitMapBackend, and a simple line chart is drawn using LineSeries. The resulting plot is saved as a PNG file, which can be further analyzed or presented.
In conclusion, the Finite Element Method is a versatile and powerful technique in computational physics. Implementing FEM in Rust involves defining element shape functions, assembling global matrices, and solving linear systems, all of which can be efficiently handled using Rust’s capabilities. The robust type system, performance-oriented features, and available numerical libraries make Rust a compelling choice for developing FEM-based simulations. Through careful implementation and appropriate use of Rust’s ecosystem, complex physical problems can be solved with accuracy and efficiency.
6.3. Numerical Linear Algebra for Computational Physics
Numerical linear algebra is a cornerstone of computational physics, providing the tools necessary to solve the large systems of linear equations that arise from discretizing differential equations via methods like Finite Difference (FDM) and Finite Element (FEM). Efficiently solving these systems is crucial because they can be extremely large, especially in three-dimensional problems or simulations involving millions of degrees of freedom.
The most common form of these systems is $Ax = b$, where $A$ is a matrix representing the discretized operator (e.g., the stiffness matrix in FEM or the finite difference matrix in FDM), $x$ is the vector of unknowns, and $b$ is the vector representing the right-hand side of the equation (e.g., external forces or boundary conditions).
Solving $Ax = b$ can be approached in several ways, depending on the properties of the matrix $A$. For small to medium-sized problems, direct methods like Gaussian elimination or LU decomposition are often used. For larger systems, iterative methods like Conjugate Gradient (for symmetric positive-definite matrices) or GMRES (for general matrices) are preferred due to their scalability and lower memory requirements.
Decomposition Techniques:
LU Decomposition: LU decomposition factors a matrix $A$ into a lower triangular matrix $L$ and an upper triangular matrix $U$, such that $A = LU$. This decomposition is particularly useful for solving linear systems multiple times with different right-hand sides because the factorization is computed once, and then back-substitution can be used to solve for different vectors $b$.
QR Decomposition: QR decomposition factors a matrix $A$ into an orthogonal matrix $Q$ and an upper triangular matrix $R$. This decomposition is especially useful in solving least-squares problems, where you want to minimize the error between the observed and predicted values.
Eigenvalue Problems: Eigenvalue problems are fundamental in many areas of physics, particularly in stability analysis, vibration analysis, and quantum mechanics. Finding the eigenvalues and eigenvectors of a matrix $A$ involves solving the characteristic equation $Av = \lambda v$, where $\lambda$ is an eigenvalue and $v$ is the corresponding eigenvector. Efficient algorithms for computing eigenvalues include the power method, QR algorithm, and Jacobi method.
In both FDM and FEM, the discretization of a continuous problem leads to a system of linear equations. For example, in FEM, the weak form of the governing differential equation leads to a global stiffness matrix $K$ and force vector $f$, resulting in the system $Kx = f$. In FDM, the application of difference schemes to approximate derivatives similarly leads to a matrix equation.
The choice of linear solver or decomposition method depends on several factors:
Matrix Structure: If the matrix is sparse (most entries are zero), as is typical in FEM and FDM, it’s crucial to use solvers that take advantage of this sparsity. Sparse matrix solvers reduce memory usage and computational cost.
Symmetry and Positive-Definiteness: For symmetric positive-definite matrices (common in many physical problems), specialized solvers like the Conjugate Gradient method are more efficient.
Size of the System: For very large systems, iterative methods are often preferred over direct methods due to their lower memory requirements and ability to handle large datasets efficiently.
Trade-offs between different solvers and decompositions involve considerations of computational efficiency, memory usage, and numerical stability. For example, while LU decomposition is stable and reliable, it can be computationally expensive for large systems, making iterative methods more attractive in such cases.
Rust has several libraries that facilitate numerical linear algebra, with ndarray and nalgebra being two of the most prominent. These libraries provide efficient implementations of matrix operations, linear solvers, and decompositions, enabling the development of high-performance computational physics simulations.
Using nalgebra for Linear Algebra Operations:
nalgebra is a comprehensive linear algebra library that supports matrix and vector operations, decompositions, and solvers. Here’s how you can use nalgebra to perform an LU decomposition and solve a linear system:
use nalgebra::{DMatrix, DVector};
fn main() {
// Define a 3x3 matrix A.
let a = DMatrix::from_row_slice(3, 3, &[
4.0, 1.0, 2.0,
1.0, 3.0, 1.0,
2.0, 1.0, 5.0,
]);
// Define a vector b, representing the right-hand side.
let b = DVector::from_row_slice(&[9.0, 7.0, 13.0]);
// Perform LU decomposition and solve the linear system A x = b.
let lu = a.lu();
let x = lu.solve(&b).unwrap();
println!("Solution: {}", x);
}
In this example, we define a $3\times 3$ matrix $A$ and a vector $b$. We then perform an LU decomposition of $A$ using nalgebra’s lu() method and solve the linear system $Ax = b$. The solution vector $x$ is printed as the result.
Using ndarray for Matrix Operations:
ndarray is another powerful library in Rust, particularly useful for handling large, multi-dimensional arrays and matrices. It is well-suited for numerical computations involving data stored in arrays:
use ndarray::array;
use ndarray::Array2;
use ndarray_linalg::Solve;
fn main() {
// Define a 3x3 matrix using ndarray.
let a: Array2<f64> = array![
[4.0, 1.0, 2.0],
[1.0, 3.0, 1.0],
[2.0, 1.0, 5.0]
];
// Define a vector representing the right-hand side.
let b = array![9.0, 7.0, 13.0];
// Solve the linear system A * x = b
match a.solve(&b) {
Ok(x) => println!("Solution: {:?}", x),
Err(err) => eprintln!("Failed to solve the system: {}", err),
}
}
Here, ndarray is used to create a $3\times 3$ matrix and a vector. The Solve trait from ndarray-linalg is employed to solve the linear system $Ax = b$. The solution vector xxx is output, demonstrating the ease of integrating linear algebra into Rust programs.
Coding Eigenvalue Problems:
Eigenvalue problems are essential in various areas of computational physics, such as vibration analysis and quantum mechanics. nalgebra supports eigenvalue computations as follows:
use nalgebra::{DMatrix, SymmetricEigen};
fn main() {
// Define a symmetric 3x3 matrix.
let a = DMatrix::from_row_slice(3, 3, &[
4.0, 1.0, 2.0,
1.0, 3.0, 1.0,
2.0, 1.0, 5.0,
]);
// Compute the eigenvalues and eigenvectors.
let eig = SymmetricEigen::new(a);
println!("Eigenvalues: {}", eig.eigenvalues);
println!("Eigenvectors: {}", eig.eigenvectors);
}
This example shows how to compute the eigenvalues and eigenvectors of a symmetric matrix using nalgebra. The SymmetricEigen structure provides access to the computed eigenvalues and corresponding eigenvectors, which are crucial in many physics applications.
In summary, numerical linear algebra is a critical component of computational physics, enabling the efficient solution of linear systems, matrix decompositions, and eigenvalue problems. Rust’s libraries, such as nalgebra and ndarray, offer robust tools for implementing these operations, making it possible to develop high-performance, scalable simulations. By integrating these tools into Rust programs, physicists and engineers can harness the power of modern numerical methods to solve complex physical problems with precision and efficiency.
6.4. Error Analysis and Validation
Error analysis is a fundamental aspect of computational physics, especially when employing numerical techniques such as finite difference (FDM) or finite element (FEM) methods. In these approaches, solutions to partial differential equations (PDEs) are approximated numerically, which introduces errors. These errors primarily stem from two sources: discretization (or truncation) errors and round-off errors.
Discretization errors occur when a continuous domain or function is represented by a discrete set of points or elements. For example, in FDM, derivatives are approximated by finite differences. In FEM, the continuous solution space is approximated using a finite number of elements and shape functions. The error introduced when the exact mathematical model is replaced by its discrete approximation is known as truncation error.
Round-off errors arise from the finite precision of floating-point representations. Since computers represent real numbers using a fixed number of binary digits (according to the IEEE 754 standard), many real numbers must be rounded to the nearest representable value. Over the course of many arithmetic operations, these small discrepancies can accumulate, potentially leading to significant deviations from the true result.
Understanding how these errors propagate through numerical computations is crucial. It allows you to design algorithms that are both robust and reliable. In practice, error estimation is often achieved by comparing numerical solutions at different levels of refinement—for example, using a finer mesh in FEM or a smaller grid spacing in FDM—and by employing analytical error bounds.
Validation is the process of confirming that the numerical method accurately represents the underlying physical problem. This can be done by comparing numerical results to known analytical solutions or benchmark problems. In heat conduction, for instance, one might compare the computed temperature distribution in a rod to the analytical solution under similar boundary conditions. When analytical solutions are not available, benchmark problems with well-documented numerical results can serve as a reference.
Mesh refinement and time-stepping are critical factors in controlling error. Refining the mesh (or grid) generally reduces discretization error but increases computational cost. Similarly, in time-dependent problems, using a smaller time step can improve accuracy but may also lead to a higher computational load. Balancing these trade-offs requires careful analysis and often involves iterative convergence studies.
Implementing error estimation and validation routines in Rust means writing code that not only performs the numerical computations but also compares the results against benchmark or analytical solutions. Below are some examples demonstrating how you can approach error analysis in Rust.
Example 1: Computing the L2 Error
The following function computes the L2 norm of the error between numerical and analytical solutions:
fn compute_error(numerical: &[f64], analytical: &[f64]) -> f64 {
let mut error = 0.0;
for (num, ana) in numerical.iter().zip(analytical.iter()) {
error += (num - ana).powi(2);
}
(error / numerical.len() as f64).sqrt()
}
fn main() {
// Example numerical and analytical solutions
let numerical = vec![1.0, 1.5, 2.0, 2.5, 3.0];
let analytical = vec![1.0, 1.4, 2.1, 2.4, 3.1];
let error = compute_error(&numerical, &analytical);
println!("Computed L2 error: {}", error);
}
This code calculates the root mean square (L2 norm) of the difference between two solution sets, thereby quantifying the overall error in the numerical solution.
Example 2: Validating Against an Analytical Solution
The next example defines a routine that computes the maximum absolute error between a numerical solution and an analytical solution evaluated at specified grid points:
fn validate_against_analytical(
numerical: &[f64],
analytical_fn: &dyn Fn(f64) -> f64,
grid_points: &[f64],
) -> f64 {
let mut max_error = 0.0;
for (i, &point) in grid_points.iter().enumerate() {
let analytical_value = analytical_fn(point);
let error = (numerical[i] - analytical_value).abs();
if error > max_error {
max_error = error;
}
}
max_error
}
fn main() {
let grid_points = vec![0.0, 0.25, 0.5, 0.75, 1.0];
let numerical = vec![0.0, 0.24, 0.47, 0.7, 0.93];
// Analytical solution: u(x) = x
let analytical_fn = |x: f64| x;
let max_error = validate_against_analytical(&numerical, &analytical_fn, &grid_points);
println!("Maximum error against analytical solution: {}", max_error);
}
In this snippet, the validate_against_analytical function iterates over a set of grid points, computes the analytical value using the provided function, and then compares it to the corresponding numerical result. The maximum error observed over the grid is reported, which provides a measure of the worst-case deviation from the expected solution.
Testing and Benchmarking Error Metrics
To ensure your error analysis routines work correctly and reliably, you can integrate them into Rust's built-in testing framework:
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn test_error_computation() {
let numerical = vec![1.0, 1.5, 2.0, 2.5, 3.0];
let analytical = vec![1.0, 1.4, 2.1, 2.4, 3.1];
let error = compute_error(&numerical, &analytical);
assert!(error < 0.1, "Error should be less than 0.1");
}
#[test]
fn test_validation_against_linear() {
let grid_points = vec![0.0, 0.25, 0.5, 0.75, 1.0];
let numerical = vec![0.0, 0.24, 0.47, 0.7, 0.93];
let analytical_fn = |x: f64| x;
let max_error = validate_against_analytical(&numerical, &analytical_fn, &grid_points);
assert!(max_error < 0.1, "Max error should be less than 0.1");
}
}
These tests use Rust’s #[test] attribute to verify that the error computation routines produce results within expected limits. Automated testing is crucial in a scientific computing environment to ensure that any changes in the numerical algorithms do not inadvertently degrade accuracy.
Error analysis and validation are essential in ensuring the accuracy and stability of numerical methods in computational physics. By quantifying errors—whether they arise from discretization, truncation, or round-off—and systematically comparing numerical results to analytical benchmarks, you can maintain the reliability of your simulations. Rust's strong type system, together with its ecosystem of libraries such as rug for arbitrary precision and ndarray for robust numerical operations, provides the necessary tools to implement advanced error analysis routines. Through careful error estimation, rigorous validation, and comprehensive testing, you can develop FEM or FDM codes that are both robust and accurate, ultimately leading to trustworthy simulation results.
6.5. Advanced Topics and Applications
Advanced topics and applications in computational physics require extending basic numerical methods to handle more complex, realistic scenarios. In many cases, simple discretization approaches are insufficient for handling irregular geometries, complex boundary conditions, or multi-physics interactions. In this context, advanced techniques—such as adaptive mesh refinement (AMR), coupled multi-physics solvers, and parallelization—become essential for achieving both accuracy and efficiency.
When dealing with complex geometries, traditional structured grids may not capture the intricacies of the domain. Unstructured meshes, commonly used in finite element methods (FEM), allow for flexible discretization using elements of different shapes (e.g., triangles or quadrilaterals in 2D; tetrahedra or hexahedra in 3D). Adaptive mesh refinement (AMR) is one such advanced technique. With AMR, the mesh is dynamically refined in regions where the solution exhibits sharp gradients or intricate features, while coarser elements are used where the solution is smooth. This targeted refinement optimizes computational resources by concentrating effort only where it is needed for accuracy.
Parallel computing is another powerful strategy to address the increasing computational demands of large-scale simulations. In problems that generate massive systems of equations—such as assembling the global stiffness matrix from numerous elements—parallelism can dramatically reduce computation time. Rust’s concurrency primitives and high-level data-parallel libraries like Rayon allow developers to safely distribute workload across multiple threads. For instance, the assembly process in FEM can be parallelized by having each thread compute the local stiffness matrices for a subset of elements, then merging these contributions into a global matrix.
Furthermore, many modern computational physics problems involve the coupling of different physical models. For example, a climate model might require the simultaneous solution of fluid dynamics, heat transfer, and chemical reactions. In such cases, separate solvers for each physical process are developed and then iteratively coupled to achieve a consistent multi-physics solution. Rust’s strict type system and ownership model, along with its support for safe concurrency, make it well-suited to implement these coupled systems without data races or memory safety issues.
Sometimes, it is also necessary to interface Rust with well-established numerical libraries written in languages like C or Fortran. Rust’s Foreign Function Interface (FFI) allows you to call these external libraries, harnessing their optimized routines while still benefiting from Rust’s safety and concurrency guarantees.
Below are several examples that illustrate these advanced concepts in Rust.
Parallel Assembly of the Global Stiffness Matrix
The following example demonstrates how to parallelize the assembly of a global stiffness matrix using Rayon. In practice, each element's local stiffness is computed and then merged into the global system:
use rayon::prelude::*;
use std::sync::{Arc, Mutex};
// Placeholder function that computes the local stiffness matrix for an element.
fn compute_element_stiffness() -> [[f64; 3]; 3] {
[[1.0, -0.5, -0.5],
[-0.5, 1.0, -0.5],
[-0.5, -0.5, 1.0]]
}
/// Assembles the global stiffness matrix in parallel.
/// - `n_nodes`: the total number of nodes.
/// - `elements`: a slice of elements, where each element is represented by a tuple of node indices.
/// - `stiffness`: a shared reference to the global stiffness matrix wrapped in a `Mutex`.
fn assemble_global_matrix_parallel(
n_nodes: usize,
elements: &[(usize, usize, usize)],
stiffness: Arc<Mutex<Vec<Vec<f64>>>>,
) {
elements.par_iter().for_each(|&(n1, n2, n3)| {
let element_nodes = [n1, n2, n3];
let local_stiffness = compute_element_stiffness();
// Lock the global stiffness matrix for thread-safe updates.
let mut stiffness = stiffness.lock().unwrap();
for i in 0..3 {
for j in 0..3 {
stiffness[element_nodes[i]][element_nodes[j]] += local_stiffness[i][j];
}
}
});
}
fn main() {
let n_nodes = 1000;
// Example element connectivity; in a real simulation, this would be a larger set.
let elements = vec![(0, 1, 2), (2, 3, 4), (4, 5, 6)];
let stiffness = Arc::new(Mutex::new(vec![vec![0.0; n_nodes]; n_nodes]));
// Assemble the global stiffness matrix in parallel.
assemble_global_matrix_parallel(n_nodes, &elements, Arc::clone(&stiffness));
println!("Assembled global stiffness matrix in parallel.");
}
Adaptive Mesh Refinement (AMR)
Adaptive mesh refinement dynamically increases the mesh resolution in regions where the solution error exceeds a threshold. This minimizes computational effort by focusing resources only where needed:
// Assume Mesh and Element are user-defined types representing the computational mesh.
struct Element {
// Element properties ...
}
impl Element {
// Refine this element, subdividing it into smaller elements.
fn refine(&mut self) {
// Implementation to subdivide the element goes here.
}
}
struct Mesh {
elements: Vec<Element>,
}
impl Mesh {
fn new() -> Self {
// Initialize the mesh with a coarse grid.
Mesh { elements: vec![] }
}
}
/// Refines the mesh adaptively based on an error estimator function.
/// - `error_estimator`: a function that returns the estimated error for a given element.
/// - `threshold`: the error threshold above which the element should be refined.
fn refine_mesh_adaptively(
mesh: &mut Mesh,
error_estimator: &dyn Fn(&Element) -> f64,
threshold: f64,
) {
mesh.elements.iter_mut().for_each(|element| {
let error = error_estimator(element);
if error > threshold {
element.refine();
}
});
}
fn main() {
let mut mesh = Mesh::new(); // Create an initial mesh.
let threshold = 0.01;
// Example error estimator function, which in practice would compute
// some measure of the local error in the solution.
let compute_error = |element: &Element| -> f64 {
// Placeholder: return some error metric.
0.02
};
refine_mesh_adaptively(&mut mesh, &compute_error, threshold);
println!("Mesh refined adaptively.");
}
Coupled Multi-Physics Solvers
For complex simulations involving multiple physical phenomena, you can build coupled systems where separate solvers interact iteratively. The following example outlines how a fluid solver and a thermal solver might be coupled:
struct FluidSolver {
// Fields representing fluid state
}
impl FluidSolver {
fn new() -> Self {
FluidSolver { /* Initialize fluid state */ }
}
// Solve the fluid dynamics part of the system.
fn solve(&mut self) -> Vec<f64> {
// Return an updated fluid state as a vector.
vec![1.0, 2.0, 3.0]
}
// Update the fluid source terms based on the thermal state.
fn update_source_terms(&mut self, _thermal_state: &[f64]) {
// Implementation details...
}
}
struct ThermalSolver {
// Fields representing thermal state
}
impl ThermalSolver {
fn new() -> Self {
ThermalSolver { /* Initialize thermal state */ }
}
// Update boundary conditions based on the fluid state.
fn update_boundary_conditions(&mut self, _fluid_state: &[f64]) {
// Implementation details...
}
// Solve the thermal conduction part of the system.
fn solve(&mut self) -> Vec<f64> {
// Return an updated thermal state as a vector.
vec![4.0, 5.0, 6.0]
}
}
/// Iteratively solves the coupled fluid and thermal systems.
fn solve_coupled_systems(
fluid_solver: &mut FluidSolver,
thermal_solver: &mut ThermalSolver,
iterations: usize,
) {
for _ in 0..iterations {
let fluid_state = fluid_solver.solve(); // Update fluid dynamics.
thermal_solver.update_boundary_conditions(&fluid_state);
let thermal_state = thermal_solver.solve(); // Update thermal field.
fluid_solver.update_source_terms(&thermal_state);
}
}
fn main() {
let mut fluid_solver = FluidSolver::new();
let mut thermal_solver = ThermalSolver::new();
let iterations = 10;
solve_coupled_systems(&mut fluid_solver, &mut thermal_solver, iterations);
println!("Coupled systems solved iteratively.");
}
Interfacing with External Libraries via FFI
For advanced numerical algorithms, you might want to leverage established libraries in C or Fortran. Rust’s Foreign Function Interface (FFI) provides a safe bridge to such external code. The following example shows how to call a C library function from Rust:
extern "C" {
// Declare a function defined in a C library.
fn c_library_function(input: f64) -> f64;
}
fn main() {
// Call the C library function within an unsafe block.
let result = unsafe { c_library_function(3.14) };
println!("Result from C library: {}", result);
}
In this snippet, the extern "C" block declares an external C function. The call to c_library_function is wrapped in an unsafe block because interacting with foreign code bypasses some of Rust's safety guarantees.
Advanced topics in numerical methods for computational physics extend the basic principles of FDM and FEM to address complex geometries, higher dimensions, and multi-physics interactions. Techniques such as adaptive mesh refinement (AMR), adaptive time stepping, and coupled solvers provide the flexibility and efficiency required for large-scale simulations. Rust’s powerful concurrency tools like Rayon, its safe FFI capabilities, and its robust type and memory management systems make it well-suited for these advanced applications. By leveraging these features, you can build high-performance, scalable, and reliable simulation software capable of tackling the most challenging computational physics problems.
6.6. Conclusion
In conclusion, Chapter 6 illustrates how Rust's robust language features can be harnessed to implement and optimize Finite Difference and Finite Element Methods in computational physics. By combining theoretical principles with practical Rust applications, readers are equipped to tackle complex physical simulations with accuracy and efficiency.
6.6.1. Further Learning with GenAI
These prompts will guide you through the theoretical underpinnings, Rust-specific implementations, and best practices for numerical methods in computational physics.
Provide a detailed explanation of the discretization process in finite difference methods, focusing on how continuous differential equations are transformed into discrete equations. Discuss the implications of different discretization techniques on numerical accuracy and stability, and how the choice of grid resolution, time-stepping, and finite difference schemes can impact the overall fidelity of simulations in terms of convergence rates and error control.
Discuss the theoretical differences between explicit and implicit finite difference methods, with an emphasis on their stability criteria (e.g., CFL condition), convergence properties, and practical considerations for time-stepping schemes. Explore when it is appropriate to choose one over the other, particularly in applications involving stiff differential equations, and analyze the trade-offs in computational complexity, memory usage, and numerical stability.
Illustrate the step-by-step process of implementing a 1D finite difference scheme in Rust, covering the creation of a spatial grid, application of Dirichlet or Neumann boundary conditions, and solving the resulting system of linear equations. Provide examples of both explicit and implicit schemes, and discuss how to ensure numerical stability and efficiency by leveraging Rust’s type system, memory management, and concurrency features.
Explore the implementation of a 2D finite difference method in Rust, focusing on handling complex boundary conditions (e.g., mixed or Robin boundary conditions) and refining the grid for improved accuracy. Discuss adaptive mesh techniques for regions requiring higher precision and how they can be integrated into the 2D scheme. Provide examples that demonstrate efficient memory usage, grid refinement strategies, and techniques for solving large systems of equations.
Compare different finite difference schemes, including central differences, forward differences, and backward differences, with an analysis of their accuracy, stability, and computational efficiency. Discuss how these schemes apply to various types of partial differential equations, such as parabolic, hyperbolic, and elliptic equations, and provide examples where one scheme may be more appropriate than others based on boundary conditions and problem characteristics.
Explain the process of discretizing a continuous domain into finite elements in finite element methods, detailing how the domain is divided into elements (e.g., triangular or quadrilateral elements in 2D, tetrahedral elements in 3D). Discuss how element types, mesh density, and nodal placement influence the accuracy of the approximation, and how these factors impact the solution of partial differential equations in complex geometries.
Describe the formulation of weak forms in finite element methods, including the derivation of element stiffness matrices, force vectors, and boundary conditions. Explain how these local matrices are assembled into a global stiffness matrix, and provide an implementation example in Rust that demonstrates numerical integration, shape function evaluation, and efficient matrix assembly for solving PDEs.
Provide a comprehensive guide to implementing a basic finite element method in Rust, covering the definition and computation of element shape functions, numerical integration (e.g., Gaussian quadrature), and solving the resulting system of linear equations using direct or iterative solvers. Highlight how Rust’s strong typing and safety features can prevent common errors in matrix operations and memory management during the implementation.
Discuss the challenges and strategies for implementing nonlinear finite element methods in Rust, including iterative solvers such as Newton-Raphson, update schemes for nonlinear material models, and handling nonlinearities in the system of equations (e.g., due to material properties or large deformations). Provide examples of efficient solver implementations and discuss techniques for ensuring convergence and accuracy in nonlinear systems.
Explore how finite element methods can be integrated with parallel computing techniques in Rust to handle large-scale simulations. Discuss the use of parallel matrix operations, domain decomposition techniques, and distributed computing strategies to efficiently solve large finite element problems. Provide examples leveraging Rust’s concurrency model (e.g., using Rayon or crossbeam) for scalable matrix assembly and solving large systems in parallel.
Delve into numerical linear algebra techniques used in computational physics, such as LU decomposition, QR factorization, and iterative solvers like conjugate gradient and GMRES. Discuss their applications in solving systems of linear equations arising in finite difference and finite element methods, and provide examples of implementing these techniques in Rust, highlighting performance considerations and stability.
Explain the implementation of eigenvalue problems in Rust, discussing methods for computing eigenvalues and eigenvectors (e.g., power iteration, Lanczos method) and their relevance to solving differential equations (e.g., vibration analysis, stability analysis). Provide detailed examples of how these techniques are used in physics simulations and how they can be efficiently implemented using Rust’s libraries and parallelism features.
Analyze different methods for quantifying and analyzing numerical errors in finite difference and finite element methods, including discretization errors, truncation errors, and their impact on the accuracy and stability of the solution. Provide strategies for minimizing these errors, such as mesh refinement, higher-order methods, or adaptive time-stepping, and discuss how Rust’s precise control over memory and data types can help manage and track numerical precision.
Discuss validation techniques for numerical methods, including comparing numerical solutions with analytical solutions or benchmark problems (e.g., manufactured solutions, exact solutions for simple cases). Explain how to implement validation routines in Rust to ensure correctness, consistency, and reproducibility in large-scale scientific simulations, using detailed examples of test cases and error estimation techniques.
Explore advanced techniques for extending finite difference and finite element methods to handle complex geometries, irregular meshes, and higher-dimensional problems (e.g., 3D simulations). Discuss how these techniques can be implemented in Rust, including strategies for efficient mesh generation, numerical integration, and matrix assembly for higher-dimensional PDEs.
Describe the implementation of adaptive mesh refinement techniques in finite element methods, discussing criteria for mesh refinement (e.g., error indicators, solution gradients), algorithms for refining and coarsening the mesh dynamically, and performance considerations. Provide examples of implementing adaptive refinement in Rust and optimizing for computational efficiency in large-scale simulations.
Analyze Rust’s concurrency and parallelism features, such as multithreading, message-passing, and parallel iterators, and their application to optimizing finite difference and finite element methods for performance and scalability. Discuss how Rust’s ownership model and safety features help avoid data races and memory issues in parallel processing, with examples of parallelizing matrix assembly and solving large systems of equations.
Discuss best practices for memory management and efficiency in Rust when implementing large-scale numerical simulations, including choosing appropriate data structures (e.g., sparse matrices, vectors), managing memory allocations and deallocations, and avoiding memory leaks or unnecessary overhead. Provide specific strategies for optimizing performance while maintaining Rust’s safety guarantees.
Explain how to integrate Rust implementations of finite difference and finite element methods with external numerical libraries, such as BLAS, LAPACK, or PETSc, using Rust’s Foreign Function Interface (FFI). Discuss techniques for ensuring efficient interoperability and leveraging the additional functionality and performance optimizations offered by these libraries for large-scale scientific computations.
Explore techniques for visualizing results from finite difference and finite element methods, including strategies for data handling, graphical representation, and post-processing using Rust libraries (e.g., plotters, gnuplot, or integration with Python visualization libraries like matplotlib). Discuss the importance of visualization for interpreting simulation results and how to efficiently generate visual outputs from large datasets.
Provide examples of post-processing techniques for analyzing and interpreting simulation results from finite difference and finite element methods, including data extraction (e.g., nodal values, stress tensors), statistical analysis (e.g., error quantification, sensitivity analysis), and result interpretation. Discuss how these techniques can be implemented in Rust, with examples of extracting meaningful insights from complex simulations.
Let the elegance of Rust and the intricacies of computational physics inspire you to push the boundaries of what is possible, transforming theoretical concepts into practical, high-performance solutions. Embrace this learning journey with curiosity and determination, and you'll unlock new heights of understanding and innovation in computational physics.
6.6.2. Assignments for Practice
By working through these exercises with GenAI (ChatGPT and/or Gemini), you'll enhance your ability to apply computational physics concepts and Rust programming skills at a higher level.
Exercise 6.1: Advanced 1D Finite Difference Implementation and Performance Optimization
Implement a 1D finite difference solver for a nonlinear partial differential equation, such as the Burgers' equation, in Rust. Incorporate adaptive time-stepping and grid refinement techniques. Optimize your code for performance by leveraging Rust’s concurrency features and efficient memory management practices. Use GenAI to evaluate the robustness of your implementation, including concurrency handling, and request detailed feedback on performance optimization strategies and potential improvements.
Exercise 6.2: Complex 2D Finite Difference Solver with Irregular Boundaries
Develop a 2D finite difference solver for a problem with irregular boundary conditions, such as a region with holes or varying geometries. Implement advanced numerical methods like the Conjugate Gradient method for solving the resulting linear system. Share your Rust implementation with GenAI, asking for a thorough review of how you handle irregular boundaries and the effectiveness of your solver. Request advice on improving numerical stability and accuracy.
Exercise 6.3: Finite Element Method with Higher-Order Elements and Nonlinearities
Implement a finite element method using higher-order polynomial elements (e.g., quadratic or cubic elements) for a nonlinear problem, such as nonlinear elasticity. Include the derivation of the nonlinear stiffness matrix and solution of the nonlinear system using Newton-Raphson iterations. Share your code and implementation details with GenAI, and request feedback on the accuracy of the higher-order elements and the robustness of the nonlinear solver.
Exercise 6.4: Numerical Linear Algebra: Custom Decompositions and Eigenvalue Problems
Develop custom implementations of advanced numerical linear algebra techniques, such as Singular Value Decomposition (SVD) or Eigenvalue Decomposition, in Rust. Apply these techniques to solve complex eigenvalue problems arising from finite element simulations. Use GenAI to review your custom implementations, focusing on algorithm correctness, performance optimization, and how well they integrate with your overall numerical framework.
Exercise 6.5: Parallel Computing and Large-Scale Simulations with Distributed Systems
Implement a parallel finite element method for large-scale simulations using distributed computing techniques in Rust. Design and implement efficient communication and load-balancing strategies to handle simulations across multiple nodes. Share your implementation details with GenAI, asking for a review of your parallelization approach, communication efficiency, and strategies for managing distributed computational resources. Request suggestions for improving scalability and performance.
These challenging exercises are designed to push the boundaries of your knowledge and skills in computational physics and Rust programming. By tackling these advanced problems, you will gain deeper insights and practical experience in implementing sophisticated numerical methods and optimizing performance.
Comments